
【题目】如图,O是坐标原点,过点A(﹣1,0)的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
(1)求b的值以及点D的坐标;
(2)连接BC、BD、CD,在x轴上是否存在点P,使得以A、C、P为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,说明理由.
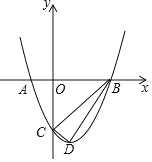
【答案】(1)b=2; D(1,﹣4).(2) 点P的坐标(0,0)(9,0).
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据相似三角形的性质,可得AP的长,根据线段的和差,可得P点坐标.
解:(1)把A(﹣1,0)代入y=x2﹣bx﹣3,得1+b﹣3=0,
解得b=2.y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4).
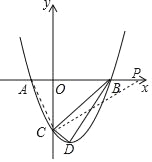
(2)如图,当y=0时,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,即A(﹣1,0),B(3,0),D(1,﹣4).
由勾股定理,得BC2=18,CD2=1+1=2,BD2=22+16=20,BC2+CD2=BD2,∠BCD=90°,
①当△APC∽△DCB时,![]() ,即
,即![]() ,解得AP=1,即P(0,0).
,解得AP=1,即P(0,0).
②当△ACP∽△DCB时,![]() ,即
,即![]() ,解得AP=10,即P′(9,0).
,解得AP=10,即P′(9,0).
综上所述:点P的坐标(0,0)(9,0).


科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
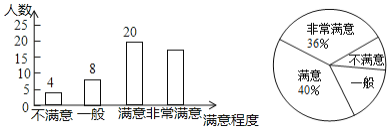
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为多少人,其中“非常满意”的人数为多少人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
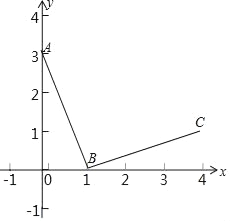
【题目】如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y=![]() 的图象G经过点C.
的图象G经过点C.
(1)请直接写出点C的坐标及k的值;
(2)若点P在图象G上,且∠POB=∠BAO,求点P的坐标;
(3)在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
方案 | 方案一 | 方案二 | 方案三 |
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
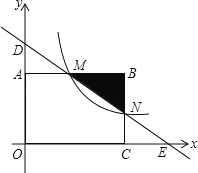
【题目】如图,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,B(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)直接写出直线DE的解析式_________;
(2)若反比例函数y=![]() (x>0)的图象与直线MN有且只有一个公共点,求m的值.
(x>0)的图象与直线MN有且只有一个公共点,求m的值.
(3)在分别过M,B的双曲线y=![]() (x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
(x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
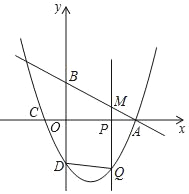
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
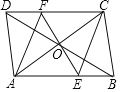
【题目】已知:四边形ABCD是平行四边形,点O是对角线AC、BD的交点,EF过点O且与AB、CD分别相交于点E、F,连接EC、AF.
(1)求证:DF=EB;(2)AF与图中哪条线段平行?请指出,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com