
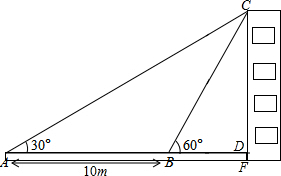
 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号). 分析 首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
解答 解:∵∠CAD=30°,∠CBD=60°,
∴∠ACB=30°,
∴∠ACB=∠CAB,
∴BA=BC=10,
在Rt△CBD中,sin∠CBD=sin60°=$\frac{CD}{CB}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{CD}{10}$,
解得:CD=5$\sqrt{3}$,
∴CF=CD+DF=CD+AE=5$\sqrt{3}$+1.
答:建筑物CF的高度为(5$\sqrt{3}$+1)m.
点评 此题考查了解直角三角形的应用,用到的知识点是三角形的外角、特殊角的三角函数值、等腰三角形的性质,要求学生能借助仰角构造直角三角形并解直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多“美妙”的性质.如关于线段比、面积比就有一些“漂亮”的结论,利用这些性质可以解决三角形的若干问题.请你利用重心的性质解决如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
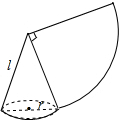 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=90°,则该圆锥的母线l长为8cm.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=90°,则该圆锥的母线l长为8cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-$\frac{1}{2}$ | B. | x≠$\frac{1}{2}$ | C. | x≤-$\frac{1}{2}$ | D. | x≠-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
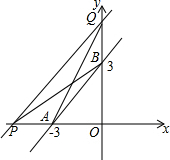 如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.
如图所示,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,3).一次函数图象与两坐标轴的交点P,Q在直线AB的同侧,且直线PQ与y轴交点在y轴正半轴上,若△QAB和△PAB的面积都等于3,求这个一次函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com