【题目】如图，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，则AB=_____.
【答案】21
【解析】
在AB上截取AE=AD，连接CE，过点C作CF⊥AB于点F，先证明△ADC≌△AEC，得出AE=AD=9，CE=CD=BC＝10的长度，再设EF=BF=x，在Rt△CFB和Rt△CFA中，由勾股定理求出x，再根据AB=AE+EF+FB求得AB的长度．
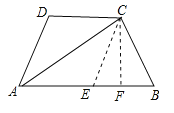
如图所示，在AB上截取AE=AD，连接CE，过点C作CF⊥AB于点F，
∵AC平分∠BAD，
∴∠DAC=∠EAC．
在△AEC和△ADC中，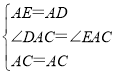
∴△ADC≌△AEC（SAS），
∴AE=AD=9，CE=CD=BC =10，
又∵CF⊥AB，
∴EF=BF，
设EF=BF=x．
∵在Rt△CFB中，∠CFB=90°，
∴CF2=CB2-BF2=102-x2，
∵在Rt△CFA中，∠CFA=90°，
∴CF2=AC2-AF2=172-（9+x）2，即102-x2=172-（9+x）2，
∴x=6，
∴AB=AE+EF+FB=9+6+6=21，
∴AB的长为21．
故答案是：21.
科目：初中数学 来源： 题型：
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的
个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：
（1）这次调查的学生共有多少名？
（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．
（3）如果要在这个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是
的直径，弦
于H，过CD延长线上一点E作的切线交AB的延长线于
切点为G，连接AG交CD于K．
求证：
；
若
，试判断AC与EF的位置关系，并说明理由；
在的条件下，若
，
，求FG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用一条直线分割一个三角形，如果能分割出等腰三角形，那么就称这条直线为该三角形的一条等腰分割线．在直角三角形ABC中，∠C＝90°，AC＝8，BC＝6．
（1）如图（1），若 O 为 AB 的中点，则直线 OC_____△ABC 的等腰分割线（填“是”或“不是”）
（2）如图（2）已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P，且 PB＝PA，请求出 CP 的长度．
（3）如图（3），在△ABC 中，点 Q 是边 AB 上的一点，如果直线 CQ 是△ABC 的等腰分割线，求线段BQ 的长度等于 ______．（直接写出答案）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
A.20°B.30°C.25°D.15°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为 1 个单位长度的小正方形组成的网格中，点 A、B、C 在小正方形的顶点上．
（1）在图中画出与△ABC 关于直线 l 成轴对称的△A′B′C′；
（2）连接 AA′，则△ACA′的面积为 ；
（3）在直线 l 上找一点 P，使 PA+PB 的长最短，则这个最短长度为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
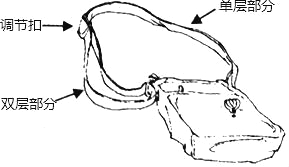
【题目】如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．小敏用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）加长或缩短．设单层部分的长度为xcm，双层部分的长度为ycm，经测量，得到如下数据：
单层部分的长度x（cm） | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y（cm） | … | 73 | 72 | 71 | … |
（1）根据表中数据的规律，完成以下表格，并直接写出y关于x的函数解析式；
（2）根据小敏的身高和习惯，挎带的长度为120cm时，背起来正合适，请求出此时单层部分的长度；
（3）设挎带的长度为lcm，求l的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠A=40°，
(1)若点P是∠ABC与∠ACB平分线的交点，求∠P的度数；
(2)若点P是∠CBD与∠BCE平分线的交点，求∠P的度数；
(3)若点P是∠ABC与∠ACF平分线的交点，求∠P的度数；
(4)若∠A=β，求(1)(2)(3)中∠P的度数(用含β的代数式表示，直接写出结果)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】李明准备进行如下操作实验，把一根长40 cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形．
(1)要使这两个正方形的面积之和等于58 cm2，李明应该怎么剪这根铁丝？
(2)李明认为这两个正方形的面积之和不可能等于48 cm2，你认为他的说法正确吗？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com