
 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
分析 (1)求得B组所占的百分比,然后根据B组有10人即可求得总人数,即样本容量,然后求得C组的人数,从而补全直方图;
(2)利用总人数乘以对应的百分比即可求解;
(3)分别求出A、E两组的人数,确定出各组的男女生人数,然后列表或画树状图,再根据概率公式计算即可得解.
解答 解:(1)∵B、E两组发言人数的比为5:2,E组发言人数占8%,
∴B组发言的人数占20%,
由直方图可知B组人数为10人,
所以,被抽查的学生人数为:10÷20%=50人,
∴样本容量为50人.
F组人数为:50×(1-6%-20%-30%-26%-8%)
=50×(1-90%)
=50×10%,
=5(人),
C组人数为:50×30%=15(人),
E组人数为:50×8%=4人
补全的直方图如图;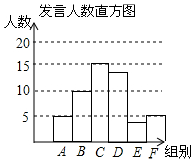
(2)F组发言的人数所占的百分比为:10%,
所以,估计全年级在这天里发言次数不少于12次的人数为:800×(8%+10%)=144(人);
(3)∵A组发言的学生为:50×6%=3人,有1位女生,
∴A组发言的有2位男生,
∵E组发言的学生:4人,
∴有2位女生,2位男生.
∴由题意可画树状图为: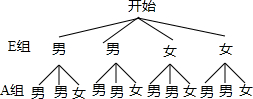
∴共有12种情况,所抽的两位学生恰都是男生的情况有4种,
∴所抽的两位学生恰好是一男一女的概率为$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,本题根据B组的人数与所占的百分比求解是解题的关键,也是本题的突破口.


科目:初中数学 来源: 题型:选择题
 如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,…则“-2016”在( )上.
如图,平面内有公共端点的四条射线OA,OB,OC,OD,从射线OA开始按逆时针方向依次在射线上写出数字2,-4,6,-8,10,-12,…则“-2016”在( )上.| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°.
如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )
如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com