练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛，正中设计一个圆形喷水池，若四周圆形和中间圆形的半径均为米，广场长为米，宽为米.

    （1）请列式表示广场空地的面积；

    （2）若休闲广场的长为500米，宽为300米，圆形花坛的半径为20米，求广场空地的面积（计算结果保留）.

    【答案】(1)、平方米；(2)、(150000－800π)平方米

    【解析】

    试题分析：(1)、空地的面积=长方形的面积减去两个圆的面积；(2)、将a、b和r代入前面的代数式进行求值即可.

    试题解析：(1)、∵广场长为米，宽为米， ∴广场的面积为：平方米，．

    四周圆形和中间圆形的面积的和为:

    ∴广场空地的面积为：平方米；

    (2)、当时，代入

    平方米

    ∴广场空地的面积为：(150000－800π)平方米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】 在数轴上与-3的距离等于5的点表示的数是 ▲ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】写出“同位角相等，两直线平行”的题设为_______，结论为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据3，6，7，4，x的平均数是5，则这组数据的中位数是（ ）
    A.4
    B.4.5
    C.5
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，正方形ABCD的边AD在y轴上，抛物线y=a（x﹣2）2﹣1经过点A、B，与x相交于点E、F，且其顶点M在CD上．

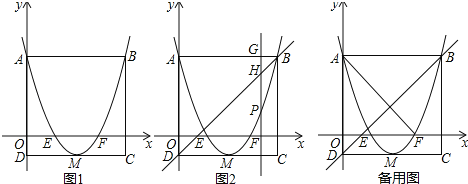
    （1）请直接写出点A的坐标 ，并写出a的值 ；

    （2）若点P是抛物线上一动点（点P不与点A、点B重合），过点P作y轴的平行线l与直线AB交于点G，与直线BD交于点H，如图2．

    ①当线段PH=2GH时，求点P的坐标；

    ②当点P在直线BD下方时，点K在直线BD上，且满足△KPH∽△AEF，求△KPH周长的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，矩形ABCD中，AB=4 cm，BC=8 cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．

    （1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

    （2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，

    ①已知点P的速度为每秒5 cm，点Q的速度为每秒4 cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

    ②若点P、Q的运动路程分别为、 （单位：cm，≠0），已知A、C、P、Q四点为顶 点的四边形是平行四边形，求与满足的数量关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】64的立方根是（ ）

    A．4 B．±4 C．8 D．±8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．

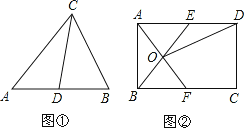
    （1）求证：△AOB和△AOE是“友好三角形”；

    （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC内接于⊙O，AB为直径，点D是弧AC上的一点，连接AD、BD，AC交BD于点F，DE⊥AB于点E，交AC于点P，∠ABD=∠CBD=∠CAD．

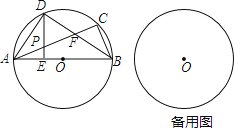
    （1）求证：PA=PD；

    （2）判断AP与PF是否相等，并说明理由；

    （3）当点C为半圆弧的中点，小李通过操作发现BF=2AD，请问小李的发现是否正确？若正确，请说明理由；若不正确，请写出BF与AD正确的关系式．

    查看答案和解析>>

    同步练习册答案