
分析 (1)设该商家第一批购进的衬衫为x件,则第二批购进的衬衫为2x件,根据单价=总价÷数量结合第二批购进衬衫的单价比第一批高10元/件,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据单价=总价÷数量可求出第一次购进衬衫的单价,根据第一、二批购进衬衫单价及数量间的关系可得出第二批购进衬衫的数量及单价,再根据总利润=单件利润×数量,即可求出两批衬衫全部售完所获得的利润.
解答 解:(1)设该商家第一批购进的衬衫为x件,则第二批购进的衬衫为2x件,
根据题意得:$\frac{13200}{x}$+10=$\frac{28800}{2x}$,
解得:x=120,
经检验,x=120是所列方程的解.
答:该商家第一批购进的衬衫为120件.
(2)该商家第一批购进的衬衫单价为13200÷120=110(元/件);
第二批购进的衬衫为2×120=240(件),单价为110+10=120(元/件).
全部售完获得的利润为(150-110)×120+(150-120)×(240-40)+(150×80%-120)×40=10800(元).
答:这样两批衬衫全部售完所获得的利润为10800元.
点评 本题考查了分式方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据数量关系,列式计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
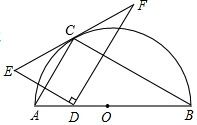 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5$\sqrt{3}$;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20$\sqrt{3}$.其中正确结论的序号是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠1=45°,∠2=45° | B. | ∠1=50°,∠2=50° | C. | ∠1=50°,∠2=40° | D. | ∠1=40°,∠2=40° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明.
已知,如图,在四边形ABCD中,AC、BD交于点O,AD∥BC,请你添加一个条件(不再添加其他线段,不再标注或使用其他字母),使AB=CD;并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,点B的坐标为(3,0),与y轴交于点C(0,-3),P是直线BC下方抛物线上的一个动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,点B的坐标为(3,0),与y轴交于点C(0,-3),P是直线BC下方抛物线上的一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com