
【题目】
(1)计算: ![]() ;
;
(2)先化简,再求值:(x+1)(2x﹣1)﹣(x﹣3)2 , 其中x=﹣2.
【答案】
(1)解:原式=4﹣2× ![]() +2
+2 ![]()
=4+ ![]() ;
;
(2)解:原式=2x2﹣x+2x﹣1﹣x2+6x﹣9
=x2+7x﹣10,
当x=﹣2时,原式=4﹣14﹣10=﹣20.
【解析】(1)根据负整数指数幂的性质和特殊角的三角函数值代入计算即可;(2)利用整式的乘法和完全平方公式展开化简后代入求值即可.
【考点精析】解答此题的关键在于理解整数指数幂的运算性质的相关知识,掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数),以及对特殊角的三角函数值的理解,了解分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0). 
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1 , y1),(x2 , y2)在抛物线上,若x1<x2<1,比较y1 , y2的大小;
(3)点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. 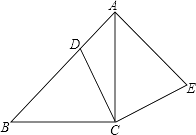
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F. 
(1)求证:DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm , 点P从点A出发,沿AB方向以每秒 ![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
A.![]()
B.2
C.2 ![]()
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com