
【题目】疫情期间,某销售商在网上销售A、B两种型号的电脑“手写板”,其进价、售价和每日销量如下表所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
A型 | 400 | 600 | 200 |
B型 | 800 | 1200 | 400 |
根据市场行情,该销售商对A型手写板降价销售,同时对B型手写板提高售价,此时发现A型手写板每降低5元就可多卖1个,B型手写板每提高5元就少卖1个.销售时保持每天销售总量不变,设其中A型手写板每天多销售x个,每天获得的总利润为y元.
(1)求y与x之间的函数关系式,并直接写出x的取值范围;
(2)要使每天的利润不低于212000元,求出x的取值范围;
(3)该销售商决定每销售一个B型手写板,就捐助a元![]() 给受“新冠疫情”影响的困难学生,若当30≤x≤40时,每天的最大利润为203400元,求a的值.
给受“新冠疫情”影响的困难学生,若当30≤x≤40时,每天的最大利润为203400元,求a的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据“总利润=A型手写板利润+B型手写板利润”即可确定函数解析式;根据600-400-5x≥0,1200-800+5x≥0即可确定自变量取值范围;
(2)把y=212000,代入函数解析式求出x值,根据函数增减性结合(1)自变量取值,即可求出x的取值;
(3)设捐款后每天的利润为w元,则w=-10x2+800x+200000-(400-x)a,即可得到w与x的关系式,确定对称轴为![]() ,结合
,结合![]() 确定对称轴取值范围
确定对称轴取值范围![]() ,结合抛物线的性质即可求出当x=40时,w最大,进而求出a.
,结合抛物线的性质即可求出当x=40时,w最大,进而求出a.
解:(1)由题意得,y=(600-400-5x)(200+x)+(1200-800+5x)(400-x)
=-10x2+800x+200000,(0≤x≤40且x为整数)
(写0<x≤40且x为整数,不扣分)
(2)x的取值范围为20≤x≤40.
理由如下:y=-10x2+800x+200000=-10(x-40)2+216000,
当y=212000时,-10(x-40)2+216000=212000,
(x-40)2=4000,x-40=±20,
解得:x=20或x=60.
要使y≥212000,
得20≤x≤60;
∵0≤x≤40,
∴20≤x≤40;
(3)设捐款后每天的利润为w元,则
w=-10x2+800x+200000-(400-x)a=-10x2+(800+a)x+200000-400a,
对称轴为![]() ,
,
∵0<a≤100,
∴![]() ,
,
∵抛物线开口向下,当30≤x≤40时,w随x的增大而增大,
当x=40时,w最大,
∴-16000+40(800+a)+200000-400a=203400,
解得a=35.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
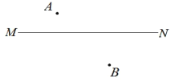
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
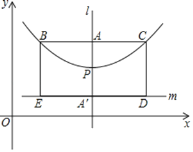
【题目】如图,在顶点为P的抛物线![]() 的对称轴l上取
的对称轴l上取![]() ,过A作
,过A作![]() 交抛物线于B,C两点(B在C左侧),点
交抛物线于B,C两点(B在C左侧),点![]() 和点A关于点P对称,过
和点A关于点P对称,过![]() 作
作![]() ,又分别过B,C作
,又分别过B,C作![]() ,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
,垂足为E,D,在这里我们把点A叫抛物线的焦点,BC叫抛物线的直径,矩形BCDE叫抛物线的焦点矩形.
(1)直接写出抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(2)求抛物线![]() 的焦点坐标及其直径;
的焦点坐标及其直径;
(3)已知抛物线![]() 的直径为
的直径为![]() ,求a的值;
,求a的值;
(4)①已知抛物线![]() 的焦点矩形的面积为2,求a的值;
的焦点矩形的面积为2,求a的值;
②直接写出抛物线![]() 的焦点矩形与抛物线
的焦点矩形与抛物线![]() 有两个公共点时m的取值范围.
有两个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级教师对试卷讲评课中学生参与的深度和广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
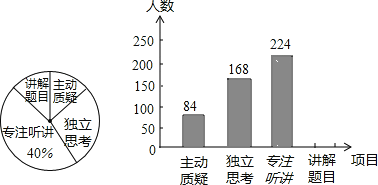
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有12000名初中学生,那么在试卷讲评课中,独立思考的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
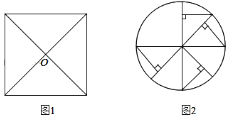
【题目】规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形 B.正五边形 C.菱形 D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);

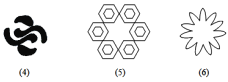
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;
A.0 B.1 C.2 D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转45°,得到
顺时针旋转45°,得到![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
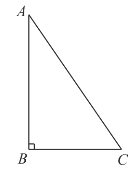
(1)根据题意补全图形;
(2)判断![]() 的形状,并证明;
的形状,并证明;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.
解法1的主要思路:
延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,可证
,可证![]() ,再证
,再证![]() 是等腰直角三角形.
是等腰直角三角形.
解法2的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,可证
,可证![]() 是等腰直角三角形,再证
是等腰直角三角形,再证![]() .
.
解法3的主要思路:
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,用含
,用含![]() 或
或![]() 的式子表示
的式子表示![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com