
 如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.
如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.分析 (1)连接OP,PM,由角平分线的定义得到∠QNP=∠PNM,由等腰三角形的性质得到∠OPN=∠ONP,等量代换得到∠OPN=∠QNP,根据平行线的判定定理得到OP∥NQ,根据平行线的性质得到OP⊥PQ,即可得到结论;
(2)连结PM,根据圆周角定理由MN是⊙O的直径得到∠MPN=90°,易证得Rt△NMP∽Rt△NPQ,然后利用相似比可计算出NQ的长.
解答 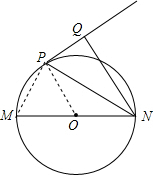 (1)证明:连接OP,PM,
(1)证明:连接OP,PM,
∵NP平分∠MNQ,
∴∠QNP=∠PNM,
∵OP=ON,
∴∠OPN=∠ONP,
∴∠OPN=∠QNP,
∴OP∥NQ,
∵NQ⊥PQ,
∴OP⊥PQ,
∴直线PQ是⊙O的切线;
(2)解:连结PM,如图,
∵MN是⊙O的直径,
∴∠MPN=90°,
∵NQ⊥PQ,
∴∠PQN=90°,
而∠MNP=∠QNP,
∴Rt△NMP∽Rt△NPQ,
∴$\frac{NP}{NQ}=\frac{MN}{NP}$,即$\frac{2\sqrt{3}}{NQ}$=$\frac{4}{2\sqrt{3}}$,
∴NQ=3.
点评 本题考查了切线的判定,角平分线的定义,平行线 的判定和性质,相似三角形的判定和性质,掌握的作出正方形是解题的关键.


科目:初中数学 来源: 题型:解答题
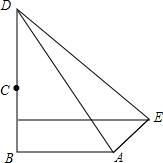 已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)
已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
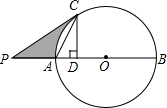 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
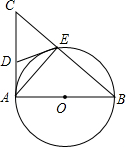 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com