
分析 首先根据题意画出图形,然后连接AC,由三角形法则,即可求得$\overrightarrow{AC}$,然后由点M、N分别是边AB、BC的中点,根据三角形中位线的性质,求得答案.
解答 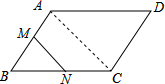 解:如图,连接AC,
解:如图,连接AC,
∵四边形ABCD是平行四边形,
∴$\overrightarrow{BC}$=$\overrightarrow{AD}$=$\overrightarrow{b}$,
∵$\overrightarrow{AB}=\overrightarrow a$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
∵点M、N分别是边AB、BC的中点,
∴$\overrightarrow{MN}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
故答案为:$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识、平行四边形的性质以及三角形中位线的性质.注意掌握三角形法则的应用是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
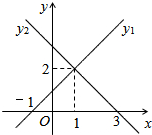 如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.
如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.
如图,己知MN是⊙O的直径,P为⊙O上一点,NP平分∠MNQ,且NQ⊥PQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
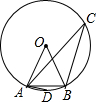 如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
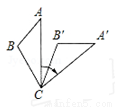
A. 30° B. 40° C. 80° D. 110°
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:单选题
当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )
和一次函数y=kx+2的图象大致是( )
A. 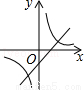 B.
B. 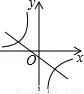
C. 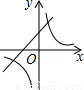 D.
D. 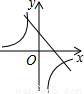
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com