
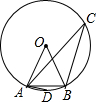
 如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )
如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=$\frac{1}{9}$πcm2;②${l_{\widehat{AB}}}=\frac{2}{9}πcm$;③∠ACB=20°;④∠ADB=140°.错误的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由正九边形的性质求出中心角的度数,再由扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质即可得出①②③正确,④错误,即可得出结果.
解答 解:∵AB为⊙O内接正九边形的一边,
∴∠AOB=$\frac{360°}{9}$=40°,
∴S扇形AOB=$\frac{40π×{1}^{2}}{360}$=$\frac{1}{9}$π(cm2),$\widehat{AB}$的长=$\frac{40π×1}{180}$=$\frac{2}{9}$π(cm);∠ACB=$\frac{1}{2}$∠AOB=20°;
∴①②③正确;∠ADB=180°-20°=160°;
∴④错误;错误的有1个,
故选:B.
点评 本题考查了正九边形的性质、扇形面积公式和弧长公式、圆周角定理以及圆内接四边形的性质;求出正九边形的性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
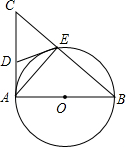 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
某中学要了解八年级学生的视力情况,在全校八年级中抽取了30名学生进行检测,在这个问题中,样本是( )
A. 八年级所有的学生 B. 被抽取的30名八年级学生
C. 八年级所有的学生的视力情况 D. 被抽取的30名八年级学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:判断题
市环保局将一个长为2×106分米,宽为4×104分米,高为8×102分米的长方体废水池中的满池废水注入正方体贮水池净化,那么请你想一想,能否恰好有一个正方体贮水池将这些废水刚好装满?若有,求出正方体贮水池的棱长;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com