
【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F. 
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
【答案】
(1)证明:∵ABCD是正方形
∴AD=BC,∠ADC=∠BCD=90°
又∵三角形CDE是等边三角形
∴CE=DE,∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE.
(2)解:∵△CDE是等边三角形,
∴CE=CD=DE,
∵四边形ABCD是正方形
∴CD=BC,
∴CE=BC,
∴△CBE为等腰三角形,且顶角∠ECB=90°﹣60°=30°
∴∠EBC= ![]() (180°﹣30°)=75°
(180°﹣30°)=75°
∵AD∥BC
∴∠AFB=∠EBC=75°.
【解析】(1)由题意正方形ABCD的边AD=DC,在等边三角形CDE中,CE=DE,∠EDC等于∠ECD,即能证其全等.(2)根据等边三角形、等腰三角形、平行线的角度关系,可以求得∠AFB的度数.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 ![]() .
.
其中正确结论的个数是( )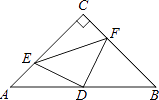
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题: 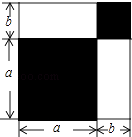
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一儿童节”促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
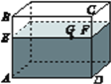
【题目】有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上. 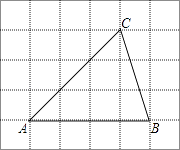
(1)△ABC的面积等于;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com