Question

【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点，与y轴交于点C，BO=CO．

（1）求抛物线的解析式；

（2）点P是第一象限抛物线上的一动点，连接AP，交y轴于点D，连接CP，设P点横坐标为t，△CDP的面积为S，求S与t之间的函数关系式（不要求写出自变量t的取值范围）；

（3）在（2）的条件下，过点P作PE⊥x轴于点E，连接PB，过点A作AF⊥PB于点F，交线段PE于点G，若点H在x轴负半轴上，PH=2GE，点M（0，m）在y轴正半轴上，连接PM、PH，∠HPM=2∠BHP，PH=2PM，求m的值．

Answer 1

【答案】（1）y=﹣x2+2x+3．（2）S =t2．（3）m=.

【解析】试题分析：（1）由ax2﹣2ax﹣3a=0时，解得x=3或﹣1，推出A（﹣1，0），B（3，0），推出OA=1，OB=3，推出OC=OB=3，推出﹣3a=3，可得a=﹣1，即可解决问题；

（2）如图1中，作PE⊥x轴于E，PK⊥y轴于K．P（t，﹣t2+2t+3，由∠PAE=∠DAO，可得tan∠PAE=tan∠DAO，可得 ，即，可得OD=3﹣t，CD=3﹣OD=t，再根据S=PKCD=计算即可；

（3）首先证明△PKM≌△PKN，推出PM=PN，MK=NK，再证明△HON≌△PKN，推出PK=HO，由∠3=∠5，可得tan∠3=tan∠5，可得 ，BE=OB﹣OE=3﹣t，即，可得GE=1，推出OH=2EG=2，推出PK=2，PE=3，推出OK=3=OC，推出点K与点C重合，由此即可解决问题．

试题解析：（1）当ax2﹣2ax﹣3a=0时，解得x=3或﹣1，

∴A（﹣1，0），B（3，0），∴OA=1，OB=3，∴OC=OB=3，∴﹣3a=3，∴a=﹣1，

∴y=﹣x2+2x+3．

（2）如图1中，作PE⊥x轴于E，PK⊥y轴于K．

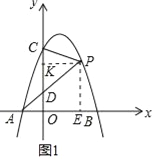
∵点P在第一象限，横坐标为t，∴P（t，﹣t2+2t+3），

∵∠PKO=∠COB=∠PEO=90°，∴四边形KPEO是矩形，∴PK=OE=t，PE=OK，

∴PE=﹣t2+2t+3，AE=t+1，

∵∠PAE=∠DAO，∴tan∠PAE=tan∠DAO，∴，∴，

∴OD=3﹣t，∴CD=3﹣OD=t，

∴S=PKCD=t2．

（3）设PH交y轴于点N．

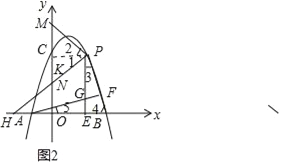
∵∠PKO=∠PKM=∠HON=90°，∴PK∥x轴，∴∠1=∠PHB，

∵∠MPH=2∠PHB，∴MPH=2∠1，即∠1=∠2，

∵∠PKM=∠PKN，PK=PK，∴△PKM≌△PKN，∴PM=PN，MK=NK，

∵PH=2PM，∴PN=HN，

∵∠HON=∠PKN，∠1=∠BHP，∴△HON≌△PKN，∴PK=HO，KN=ON，

∵AF⊥PB，∴∠AFB=90°，∴∠3+∠4=90°，

∵∠PEB=90°，∴∠4+∠5=90°，∴∠3=∠5，∴tan∠3=tan∠5，

∴，∵BE=OB﹣OE=3﹣t，∴，∴GE=1，

∴OH=2EG=2，∴PK=2，PE=3，∴OK=3=OC，∴点K与点C重合，∴KN=，

∴OM=3KN=，即m=.