
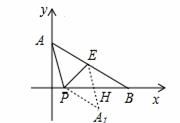
如图,在抛物线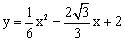 中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: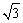 。
。
(1)求m的值;
(2)动点P从B点出发,沿x轴反方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的
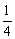 ,求此时点P的坐标。
,求此时点P的坐标。

解 :(1)∵
:(1)∵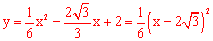 ,
,
∴B(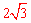 ,0)、A(0,2)、E(
,0)、A(0,2)、E( ,1)。
,1)。
∵CO:OF=2: ,
,
∴CO=﹣m,FO=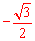 m,
m,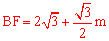 。
。
∵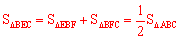 ,
,
∴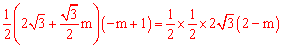 。
。
整理得:m2+m=0。∴m=﹣1或0 。
∵m<0,∴m=﹣1。
(2)在Rt△ABO中,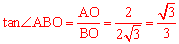 ,
,
∴∠ABO=30°,AB=2AO=4。

①当∠BPE>∠APE时,连接A1B,则对折后如图1,A1为对折后A的所落点,△EHP是重叠部分。

③当∠ BPE<∠APE时.则对折后如图2,A1为对折后A的所落点,△EH
BPE<∠APE时.则对折后如图2,A1为对折后A的所落点,△EH P是重叠部分。
P是重叠部分。
∵E为AB中点,∴S△AEP=S△BEP=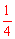 S△ABP。
S△ABP。
∵S△EHP=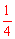 S△ABP,∴S△EBH=S△EHP=
S△ABP,∴S△EBH=S△EHP=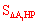 =
=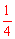 S△ABP。
S△ABP。
∴BH=HP,EH=HA1=1。
又∵BE=EA=2,∴EH
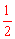 AP。∴AP=2。
AP。∴AP=2。
在△APB中,∠ABP=30°,AB=4,AP=2,
∴∠APB=90°。∴BP=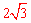 。∴点P的坐标为(
。∴点P的坐标为(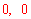 )。
)。
综上所述,点P的坐标为(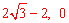 )或(
)或(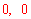 )。
)。
【考点】二次函数综合题,折叠和单动点问题,曲线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,平行四边形的判定和性质,二次函数的性质,折叠的性质,分类思想和转换思想的应用。



 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
如图①,在矩形纸片ABCD中,AB=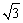
 +1,AD=
+1,AD=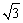
 .
.
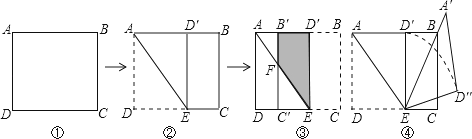
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 ;
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ;
(3)如图④ ,将图
,将图 ②中的△AE
②中的△AE D′绕点E顺时针旋转α角,得△A′ED″,使得EA′
D′绕点E顺时针旋转α角,得△A′ED″,使得EA′ 恰好经过顶点B,求弧D′D″的长.(结果保留π)
恰好经过顶点B,求弧D′D″的长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
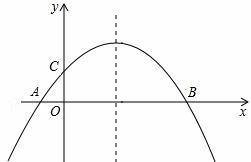
如图,抛物线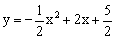 与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。
与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点 P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:
P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究: 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
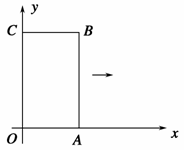
如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平 移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知菱形ABCD的边长为4,∠A=60°,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的 面积和为S1.
面积和为S1.
(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2,CF=x, .
.
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形纸片ABCD中,AB=1,BC=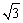 ,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
①当四边形A,CDF为矩形时,EF=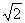 ;
;
②当EF=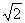 时,四边形A′CDF为矩形;
时,四边形A′CDF为矩形;
③当EF=2时,四边形BA′CD为等腰梯形;
④当四边形BA′CD 为等腰梯形时,EF=2。
为等腰梯形时,EF=2。

其中正确的是  (把所有正确结论序号都填在横线上)。
(把所有正确结论序号都填在横线上)。
查看答案和解析>>
科目:初中数学 来源: 题型:
设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反 比例函数
比例函数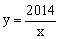 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数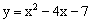 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com