
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ、DP交于点O,并分别与边CD、BC交于点F、E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD<S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的是_____.(请将正确结论的序号填写在横线上)
,其中正确结论的是_____.(请将正确结论的序号填写在横线上)

【答案】①④
【解析】
由四边形ABCD是正方形可得 AD=BC、∠DAB=∠ABC=90°,再根据全等三角形的性质可得∠P=∠Q,最后根据余角的性质可得AQ⊥DP;故①正确;根据相似三角形的性质可得AO2=ODOP,由OD≠OE,得到OA2≠OEOP;故②错误;根据全等三角形的性质得到CF=BE,DF=CE,则S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF;故③错误;根据相似三角形的性质可得BE=![]() ,求得QE=
,求得QE=![]() ,QO=
,QO=![]() ,OE=
,OE=![]() ,最后由三角函数的定义即可得到结论.
,最后由三角函数的定义即可得到结论.
解:①∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
 ,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故①正确;
②∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OEOP;故②错误;
③在△CQF与△BPE中
 ,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
 ,
,
∴△ADF≌△DCE(SAS),
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故③错误;
④∵BP=1,AB=3,
∴AP=4,
∵△PBE∽△PAD,
∴![]() ,
,
∴BE=![]() ,
,
∴QE=![]() ,
,
∵△QOE∽△PAD,
∴![]() =
=![]() ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5﹣QO=![]() ,
,
∴tan∠OAE=![]() ,故④正确,
,故④正确,
故答案为:①④.


科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情发生后,为支援疫情防控,某企业研发14条口罩生产线,生产普通防护口罩和普通N95口罩,现日总产量达170万只.已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只.
(1)将170万用科学记数法表示为 ;
(2)这14条生产线中,生产普通防护口罩和普通N95口罩的生产线分别有多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为向明中学提供午餐的某送餐公司计划每月最后一天推出学生“惊喜套餐”,现做出几款套餐后打算每班邀请一位学生代表来品尝.初三(6)班有44人(学号从1~44号),班长设计了一个推选本班代表的办法:从一副扑克牌中选取了分别标有数字1、2、3、4的四张牌.先抽取一张牌记下数字后,放回洗匀;再抽取一张牌记下数字,两个数字依次组成学生代表的学号.比如第一张抽到1,第二张抽到4,就是学号为14的这个同学作为本班代表.
(1)如果小林的学号为23,请用列表法或画出树状图的方法,求出他被抽到的概率;
(2)对初三(6)班的每位同学来说,班长设计的办法是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一段时期内对某种商品经销情况进行统计得到该商品的销售数量![]() (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价
(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价![]() (元/件,
(元/件,![]() )成反比例,销售过程中得到的部分数据如下:
)成反比例,销售过程中得到的部分数据如下:
售价 | 8 | 10 |
销售数量 | 70 | 58 |
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
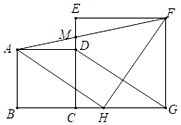
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
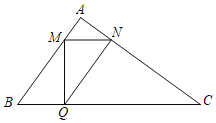
【题目】如图,在ABC中,∠A=90°,AB=3,AC=4,点M、Q分别是边AB、BC上的动点(点M不与A、B重合),且MQ⊥BC,过点M作MN∥BC.交AC于点N,连接NQ,设BQ=x.
(1)是否存在一点Q,使得四边形BMNQ为平行四边形,并说明理由;
(2)当BM=2时,求x的值;
(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
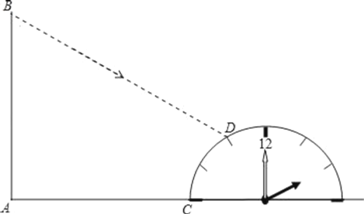
【题目】如图,某学校旗杆AB旁边有一个半侧的时钟模型,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2m,旗杆的底端A到钟面9点刻度C的距离为11m,一天小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1米长的标杆的影长1.2m.求旗杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
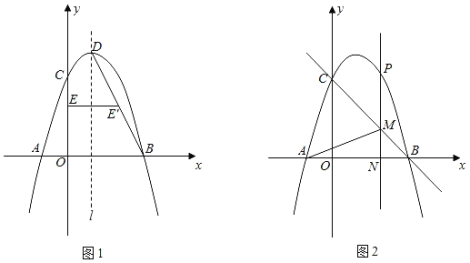
【题目】如图1,二次函数y=﹣x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l是抛物线的对称轴,D是抛物线的顶点.
(1)求该抛物线的函数表达式;
(2)如图1,连结BD,线段OC上点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;
(3)如图2,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线分别与BC交于点M,与x轴交于点N.试问:抛物线上是否存在点Q,使得△PQN与△AMN的面积相等,且线段PQ的长度最小?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com