【题目】新冠肺炎疫情发生后，为支援疫情防控，某企业研发14条口罩生产线，生产普通防护口罩和普通N95口罩，现日总产量达170万只．已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只．
（1）将170万用科学记数法表示为 ；
（2）这14条生产线中，生产普通防护口罩和普通N95口罩的生产线分别有多少条?
【答案】（1）
；（2）普通防护口罩生产线10条，普通N95口罩生产线4条．
【解析】
（1）科学记数法的表示形式为
的形式，其中
，
为整数．确定的值时，要看把原数变成
时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值
时，是正数；当原数的绝对值
时，是负数；
（2）设普通防护口罩生产线
条，普通
口罩的生产线
条，根据“口罩生产线有14条，日总产量达170万只”列出方程组求解即可．
解：（1）将170 0000用科学记数法表示为：．
故答案为：．
（2）设这14条生产线中有普通防护口罩生产线条，普通口罩的生产线条，
根据题意得：
，
解得：
，
答：这14条生产线中有普通防护口罩生产线10条，普通口罩的生产线4条．
科目：初中数学 来源： 题型：
【题目】为了满足学生的兴趣爱好，学校决定在七年级开设兴趣班，兴趣班设有四类：
围棋班；
象棋班；
书法班；
摄影班．为了便于分班，年级组随机抽查了部分学生的选课意向（每人选报一类），并绘制了如图所示的两幅统计图（不完整），请根据图中信息，解答下问题：
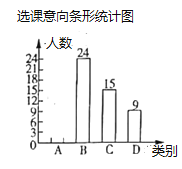
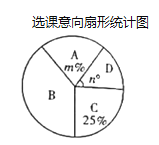
（1）求扇形统计图中
、
的值，并补全条形统计图；
（2）已知该校七年级有600名学生，学校计划开设三个“围棋班”，每班要求不超过40人，实行随机分班．
①学校的开班计划是否能满足选择“围棋班”的学生意愿，说明理由；
②展鹏、展飞是一对双胞胎，他们都选择了“围棋班”，并且希望能分到同一个班，用树状图或列表法求他们的希望得以实现的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴交于点
，与
轴交于点
，经过、两点的抛物线
与轴的另一交点
．
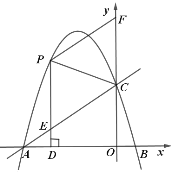
（1）求该抛物线的函数表达式；
（2）
是该抛物线上的动点，过点作
轴于点
，交
于点
，
交轴于点
，设点的横坐标为
．
①求出四边形
的周长
与
的函数表达式，并求的最大值；
②当为何值时，四边形是菱形；
③是否存在点，使得以、、为顶点的三角形与
相似？若存在，请求出满足条件的点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．
（1）求水柱所在抛物线（第一象限部分）的函数表达式；
（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？
（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+3经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，连接AD，点P是线段AD上一个动点（不与A，D重合），过点P作y轴的垂线，垂足点为E，连接AE．
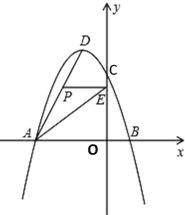
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
：
(
为常数)的顶点为
．
(1)求点的坐标；(用含的式子表示)
(2)在同一平面直角坐标系中，存在函数图象
，点
在图象上，点
在抛物线上，对于任意的实数
，都有点
，
关于点
对称．
①当
时，求图象对应函数的解析式；
②当
时，都有
成立，结合图象，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
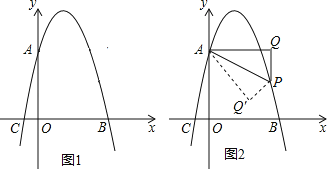
【题目】如图1，已知抛物线y＝﹣x2+bx+c交y轴于点A(0，4)，交x轴于点B(4，0)，点P是抛物线上一动点，试过点P作x轴的垂线1，再过点A作1的垂线，垂足为Q，连接AP．
(1)求抛物线的函数表达式和点C的坐标；
(2)若△AQP∽△AOC，求点P的横坐标；
(3)如图2，当点P位于抛物线的对称轴的右侧时，若将△APQ沿AP对折，点Q的对应点为点Q′，请直接写出当点Q′落在坐标轴上时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一个函数，自变量x取a时，函数值y也等于a，我们称a为这个函数的不动点.如果二次函数y＝x2+2x+c有两个相异的不动点x1、x2，且x1＜1＜x2，则c的取值范围是( )
A. c＜﹣3B. c＜﹣2C. c＜
D. c＜1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长是3，BP＝CQ，连接AQ、DP交于点O，并分别与边CD、BC交于点F、E，连接AE，下列结论：①AQ⊥DP；②OA2＝OEOP；③S△AOD＜S四边形OECF；④当BP＝1时，tan∠OAE＝
，其中正确结论的是_____．（请将正确结论的序号填写在横线上）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com