
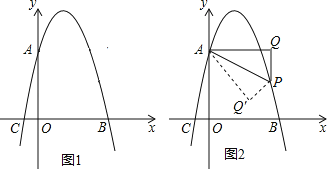
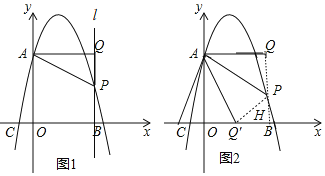
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
【答案】(1)y=﹣x2+3x+4;(﹣1,0);(2)P的横坐标为![]() 或
或![]() .(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
.(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
【解析】
(1)利用待定系数法求抛物线解析式,然后利用抛物线解析式得到一元二次方程,通过解一元二次方程得到C点坐标;
(2)利用△AQP∽△AOC得到AQ=4PQ,设P(m,﹣m2+3m+4),所以m=4|4﹣(﹣m2+3m+4|,然后解方程4(m2﹣3m)=m和方程4(m2﹣3m)=﹣m得P点坐标;
(3)设P(m,﹣m2+3m+4)(m>![]() ),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
解:(1)把A(0,4),B(4,0)分别代入y=﹣x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+3x+4,
当y=0时,﹣x2+3x+4=0,解得x1=﹣1,x2=4,
∴C(﹣1,0);
故答案为y=﹣x2+3x+4;(﹣1,0);
(2)∵△AQP∽△AOC,
∴![]() ,
,
∴![]() ,即AQ=4PQ,
,即AQ=4PQ,
设P(m,﹣m2+3m+4),
∴m=4|4﹣(﹣m2+3m+4|,即4|m2﹣3m|=m,
解方程4(m2﹣3m)=m得m1=0(舍去),m2=![]() ,此时P点横坐标为
,此时P点横坐标为![]() ;
;
解方程4(m2﹣3m)=﹣m得m1=0(舍去),m2=![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
综上所述,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)设![]() ,
,
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4﹣(﹣m2+3m+4)=m2﹣3m,
∵△APQ沿AP对折,点Q的对应点为点Q',
∴∠AQ′P=∠AQP=90°,AQ′=AQ=m,PQ′=PQ=m2﹣3m,
∵∠AQ′O=∠Q′PH,
∴Rt△AOQ′∽Rt△Q′HP,
∴![]() ,即
,即![]() ,解得Q′H=4m﹣12,
,解得Q′H=4m﹣12,
∴OQ′=m﹣(4m﹣12)=12﹣3m,
在Rt△AOQ′中,42+(12﹣3m)2=m2,
整理得m2﹣9m+20=0,解得m1=4,m2=5,此时P点坐标为(4,0)或(5,﹣6);
当点Q′落在y轴上,则点A、Q′、P、Q所组成的四边形为正方形,
∴PQ=AQ′,
即|m2﹣3m|=m,
解方程m2﹣3m=m得m1=0(舍去),m2=4,此时P点坐标为(4,0);
解方程m2﹣3m=﹣m得m1=0(舍去),m2=2,此时P点坐标为(2,6),
综上所述,点P的坐标为(4,0)或(5,﹣6)或(2,6)


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.
(1)用含x的代数式表示:第一次购进手链的数量为 条;
(2)求x的值;
(3)不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于四个数“![]() ,
,![]() ,
,![]() ,
,![]() ”及四种运算“
”及四种运算“![]() ,
,![]() ,
,![]() ,
,![]() ”,列算式解答:
”,列算式解答:
(1)求这四个数的和;
(2)在这四个数中选出两个数,按要求进行下列计算,使得:
①两数差的结果最小;
②两数积的结果最大;
(3)在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,使运算结果等于没选的那个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情发生后,为支援疫情防控,某企业研发14条口罩生产线,生产普通防护口罩和普通N95口罩,现日总产量达170万只.已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只.
(1)将170万用科学记数法表示为 ;
(2)这14条生产线中,生产普通防护口罩和普通N95口罩的生产线分别有多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
组别 | A | B | C | D | E |
分组(元) | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x<120 | 120≤x<150 |
频数 | 4 | a | 20 | 8 | 2 |
请根据以上图标,解答下列问题:
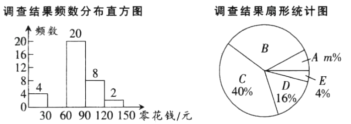
(1)填空:这次调查的样本容量是 ,a= ,m= ;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形B的圆心角度数;
(4)该校共有1000人,请估计每月零花钱的数额x在30≤x<90范围的人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
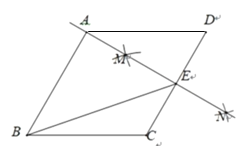
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
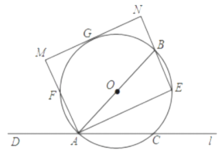
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为向明中学提供午餐的某送餐公司计划每月最后一天推出学生“惊喜套餐”,现做出几款套餐后打算每班邀请一位学生代表来品尝.初三(6)班有44人(学号从1~44号),班长设计了一个推选本班代表的办法:从一副扑克牌中选取了分别标有数字1、2、3、4的四张牌.先抽取一张牌记下数字后,放回洗匀;再抽取一张牌记下数字,两个数字依次组成学生代表的学号.比如第一张抽到1,第二张抽到4,就是学号为14的这个同学作为本班代表.
(1)如果小林的学号为23,请用列表法或画出树状图的方法,求出他被抽到的概率;
(2)对初三(6)班的每位同学来说,班长设计的办法是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
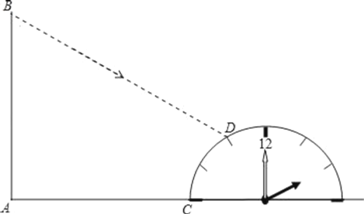
【题目】如图,某学校旗杆AB旁边有一个半侧的时钟模型,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2m,旗杆的底端A到钟面9点刻度C的距离为11m,一天小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1米长的标杆的影长1.2m.求旗杆AB的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com