
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
组别 | A | B | C | D | E |
分组(元) | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x<120 | 120≤x<150 |
频数 | 4 | a | 20 | 8 | 2 |
请根据以上图标,解答下列问题:
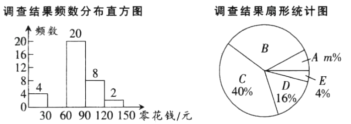
(1)填空:这次调查的样本容量是 ,a= ,m= ;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形B的圆心角度数;
(4)该校共有1000人,请估计每月零花钱的数额x在30≤x<90范围的人数;
【答案】(1)50、16、8;(2)见解析;(3)115.2°;(4)720人
【解析】
(1)根据C组频数及其所占百分比可得总人数,总人数减去其他各组人数即可求得B组人数,再用A组人数除以总人数可得m的值;
(2)根据以上所求结果即可补全直方图;
(3)用360°乘以B组人数所占比例;
(4)总人数乘以样本中B、C组人数之和所占比例即可求解.
(1)这次调查的样本容量是20÷40%=50,
则a=50-(4+20+8+2)=16,m%=![]() ×100%=8%,即m=8;
×100%=8%,即m=8;
(2)补全频数直方图如下: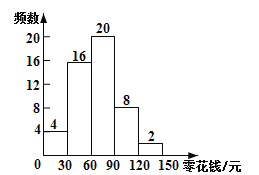
(3)扇形统计图中扇形B的圆心角度数为360°×![]() =115.2°;
=115.2°;
(4)估计每月零花钱的数额x在30≤x<90范围的人数为1000×![]() =720人.
=720人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依托独特的气候资源,天然肥沃的优质土壤,广元市大力推广蔬菜种植,疫情防控期间,某蔬菜种植基地通过电商平台将蔬菜销往全国各地,销量大幅度提升.该基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)求改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元;
(2)已知改造1个甲种型号大棚需要5天,改造1个乙种型号大棚需要3天,该基地计划用126万元资金改造一定数量的两种型号蔬菜大棚,且要求改造时间总共不超过50天,请问:有几种改造方案?哪种方案改造时间最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点,与y轴交于点C,其顶点为D,连接AD,点P是线段AD上一个动点(不与A,D重合),过点P作y轴的垂线,垂足点为E,连接AE.
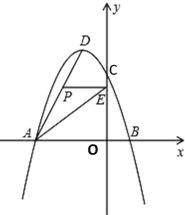
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
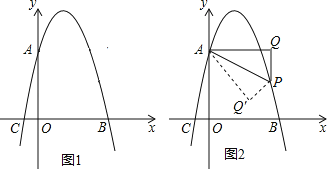
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.机场对乘客进行安检不能采用抽样调查
B.一组数据10,11,12,9,8的平均数是10,方差是2
C.“清明时节雨纷纷”是随机事件
D.一组数据6,5,3,5,4的众数是5,中位数是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com