练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】对于四个数“，，，”及四种运算“，，，”，列算式解答：

    （1）求这四个数的和；

    （2）在这四个数中选出两个数，按要求进行下列计算，使得：

    ①两数差的结果最小；

    ②两数积的结果最大；

    （3）在这四个数中选出三个数，在四种运算中选出两种，组成一个算式，使运算结果等于没选的那个数．

    【答案】（1）；（2）①；②；（3）（答案不唯一）．

    【解析】

    （1）将题目中的数据相加即可解答本题；
    （2）①根据题目中的数字，可以写出结果最小的算式；
    ②根据题目中的数字，可以写出结果最大的算式；
    （3）本题答案不唯一，主要符合题意即可．

    解：（1）（-8）+（-2）+1+3=-6；

    （2）由题目中的数字可得，

    ①，结果最小；

    ②，结果最大；

    （3）由题目中的数字可得，

    （答案不唯一）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图象与反比例函数在第一象限的图象交于和两点，与轴交于点连接

    （1）求反比例函数的解析式；

    （2）若点在轴上，且，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是双曲线y＝上的动点，连结AO并延长交双曲线于点B，将线段AB绕B顺时针旋转60°得到线段BC，点C在双曲线y＝上的运动，则k＝____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点，经过、两点的抛物线与轴的另一交点．

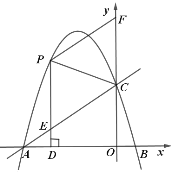
    （1）求该抛物线的函数表达式；

    （2）是该抛物线上的动点，过点作轴于点，交于点，交轴于点，设点的横坐标为．

    ①求出四边形的周长与的函数表达式，并求的最大值；

    ②当为何值时，四边形是菱形；

    ③是否存在点，使得以、、为顶点的三角形与相似？若存在，请求出满足条件的点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】依托独特的气候资源，天然肥沃的优质土壤，广元市大力推广蔬菜种植，疫情防控期间，某蔬菜种植基地通过电商平台将蔬菜销往全国各地，销量大幅度提升．该基地为提高蔬菜产量，计划对甲、乙两种型号蔬菜大棚进行改造，根据预算，改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元，改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元．

    （1）求改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元；

    （2）已知改造1个甲种型号大棚需要5天，改造1个乙种型号大棚需要3天，该基地计划用126万元资金改造一定数量的两种型号蔬菜大棚，且要求改造时间总共不超过50天，请问：有几种改造方案？哪种方案改造时间最短？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

    （1）求水柱所在抛物线（第一象限部分）的函数表达式；

    （2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

    （3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+3经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，连接AD，点P是线段AD上一个动点（不与A，D重合），过点P作y轴的垂线，垂足点为E，连接AE．

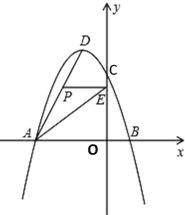
    （1）求抛物线的函数解析式，并写出顶点D的坐标；

    （2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

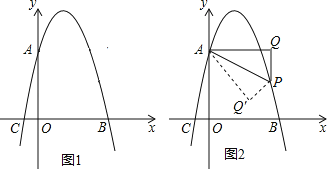
    【题目】如图1，已知抛物线y＝﹣x2+bx+c交y轴于点A(0，4)，交x轴于点B(4，0)，点P是抛物线上一动点，试过点P作x轴的垂线1，再过点A作1的垂线，垂足为Q，连接AP．

    (1)求抛物线的函数表达式和点C的坐标；

    (2)若△AQP∽△AOC，求点P的横坐标；

    (3)如图2，当点P位于抛物线的对称轴的右侧时，若将△APQ沿AP对折，点Q的对应点为点Q′，请直接写出当点Q′落在坐标轴上时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）：有同样大小正方形256个，拼成如图1所示的的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过多少个小正方形？

    （问题探究）：我们先考虑以下简单的情况：一条直线穿越一个正方形的情况．（如图2）

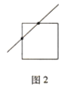
    从图中我们可以看出，当一条直线穿过一个小正方形时，这条直线最多与正方形上、下、左、右四条边中的两个边相交，所以当一条直线穿过一个小正方形时，这条直线会与其中某两条边产生两个交点，并且以两个交点为顶点的线段会全部落在小正方形内．

    这就启发我们：为了求出直线最多穿过多少个小正方形，我们可以转而去考虑当直线穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段，进而通过线段的根数确定下正方形的个数．

    再让我们来考虑正方形的情况（如图3）：

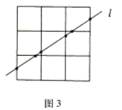
    为了让直线穿越更多的小正方形，我们不妨假设直线右上方至左下方穿过一个的正方形，我们从两个方向来分析直线穿过正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的两条线段；从左右来看，这条直线最多可穿过左右平行的四条线段；这样直线最多可穿过的大正方形中的六条线段，从而直线上会产生6个交点，这6个交点之间的5条线段，每条会落在一个不同的正方形内，因此直线最多能经过5个小正方形．

    （问题解决）：

    （1）有同样大小的小正方形16个，拼成如图4所示的的一个大的正方形．如果用一条直线穿过这个大正方形的话，最多可以穿过_________个小正方形．

    （2）有同样大小的小正方形256个，拼成的一个大的正方形.如果用一条直线穿过这个大正方形的话，最多可以穿过___________个小正方形．

    （3）如果用一条直线穿过的大正方形的话，最多可以穿过___________个小正方形．

    （问题拓展）：

    （4）如果用一条直线穿过的大长方形的话（如图5），最多可以穿过个___________小正方形．

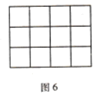
    （5）如果用一条直线穿过的大长方形的话（如图6），最多可以穿过___________个小正方形．

    （6）如果用一条直线穿过的大长方形的话，最多可以穿过________个小正方形．

    （类比探究）：

    由二维的平面我们可以联想到三维的立体空间，平面中的正方形中四条边可联想到正方体中的正方形的六个面，类比上面问题解决的方法解决如下问题：

    （7）如图7有同样大小的小正方体8个，拼成如图所示的的一个大的正方体.如果用一条直线穿过这个大正方体的话，最多可以穿过___________个小正方体．

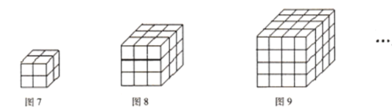
    （8）如果用一条直线穿过的大正方体的话，最多可以穿过_________个小正方体．

    查看答案和解析>>

    同步练习册答案