
【题目】如图,点A是双曲线y=![]() 上的动点,连结AO并延长交双曲线于点B,将线段AB绕B顺时针旋转60°得到线段BC,点C在双曲线y=
上的动点,连结AO并延长交双曲线于点B,将线段AB绕B顺时针旋转60°得到线段BC,点C在双曲线y=![]() 上的运动,则k=____.
上的运动,则k=____.

【答案】﹣9.
【解析】
连接OC,易证AO⊥OC,OC=![]() OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF=
OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF=![]() AE,FC=
AE,FC=![]() EO.设点A坐标为(a,b),则ab=3,设点C坐标为(x,y),从而有FCOF=-xy=-9,即k=xy=-9.
EO.设点A坐标为(a,b),则ab=3,设点C坐标为(x,y),从而有FCOF=-xy=-9,即k=xy=-9.
解:∵双曲线y=![]() 关于原点对称,
关于原点对称,
∴点A与点B关于原点对称.
∴OA=OB.
连接OC,AC,如图所示.
∵将线段AB绕B顺时针旋转60°得到线段BC,
∴△ABC是等边三角形,OA=OB,
∴OC⊥AB,∠BAC=60°,
∴tan∠OAC=![]() =
=![]() ,
,
∴OC=![]() OA.
OA.
过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,
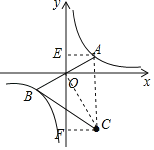
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF,
∴△AEO∽△OFC.
∴![]() .
.
∵OC=![]() OA,
OA,
∴OF=![]() AE,FC=
AE,FC=![]() EO.
EO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OF=![]() AE=
AE=![]() a,FC=
a,FC=![]() EO=
EO=![]() b.
b.
∵点A在双曲线y=![]() 上,
上,
∴ab=3.
∴FCOF=![]() b
b![]() a=3ab=9,
a=3ab=9,
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FCOF=x(﹣y)=﹣xy=9.
∴xy=﹣9.
∵点C在双曲线y=![]() 上,
上,
∴k=xy=﹣9.
故答案为:﹣9.


科目:初中数学 来源: 题型:
【题目】如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
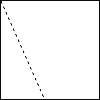
A.直角三角形B.平行四边形C.菱形D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2020年元月起,收费标准上调为餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2020年处理的这两种垃圾数量与2019年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2019年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2020年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2020年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.
(1)用含x的代数式表示:第一次购进手链的数量为 条;
(2)求x的值;
(3)不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2).
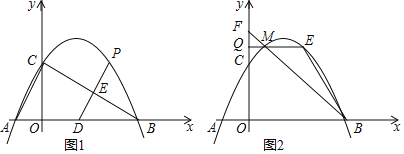
(1)求抛物线的解析式;
(2)如图1,点D的坐标为(2,0),点P是该抛物线第一象限上的一个动点,连接DP交BC于点E.当△BDE是等腰三角形时,直接写出此时点E的坐标;
(3)如图2,点M(m,n)是抛物线上位于对称轴的左侧且不在坐标轴上的动点,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F,当S△MFQ:S△MEB=1:3时,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于四个数“![]() ,
,![]() ,
,![]() ,
,![]() ”及四种运算“
”及四种运算“![]() ,
,![]() ,
,![]() ,
,![]() ”,列算式解答:
”,列算式解答:
(1)求这四个数的和;
(2)在这四个数中选出两个数,按要求进行下列计算,使得:
①两数差的结果最小;
②两数积的结果最大;
(3)在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,使运算结果等于没选的那个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
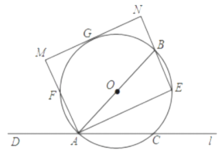
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com