
����Ŀ��2019��ij��ҵ���ͳ�����������25Ԫ/�֣���������������16Ԫ/�ֱ�����֧���ͳ��ͽ�������������5200Ԫ����2020��Ԫ�����շѱ��ϵ�Ϊ�ͳ�����������100Ԫ/�֣���������������30Ԫ/�֣�������ҵ2020�괦��������������������2019�����û�б仯����Ҫ��֧������������8800Ԫ.
��1������ҵ2019�괦���IJͳ������ͽ������������ٶ֣�
��2������ҵ�ƻ�2020�꽫���������������������ٵ�240�֣��ҽ��������������������ͳ�������������3������2020�����ҵ������Ҫ֧�����������������ѹ�����Ԫ��
���𰸡���1��2019�����ҵ�����IJͳ�����Ϊ80�֣���������Ϊ200��.��2��11400Ԫ.
��������
��1����2019�����ҵ�����IJͳ�����Ϊx�֣���������Ϊy�֣����������г������飬��˷����鼴�ɵõ��𰸣�
��2����2020�����ҵ�����IJͳ�����Ϊa�֣���������Ϊb�֣���֧����������������������cԪ��������2020�꽫���������������������ٵ�240�֣��ҽ��������������������ͳ�������������3���������a��ȡֵ��Χ�����г�c����a��һ�κ���������һ�κ����������Լ�������
�⣺��1����2019�����ҵ�����IJͳ�����Ϊx�֣���������Ϊy�֣����������
![]() ��
��
���![]() ��
��
��2019�����ҵ�����IJͳ�����Ϊ80�֣���������Ϊ200�֣�
��2����2020�����ҵ�����IJͳ�����Ϊa�֣���������Ϊb�֣���֧����������������������cԪ�����������a+b=240��b��3a��
���a��60��
����c=100a+30b=100a+30��240-a��=70a+7200��
����c��ֵ��a�����������
���Ե�a=60ʱ��c��С����СֵΪ70��60+7200=11400Ԫ��
��2020�����ҵ������Ҫ֧�����������������ѹ�11400Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() �ֱ�������
�ֱ�������![]() ��
��![]() �ϵĵ㣮
�ϵĵ㣮
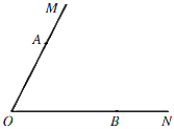
��1���߹���ͼ����![]() ���ڲ�ȷ��һ��
���ڲ�ȷ��һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ����������ͼ�ۼ�����д������
����������ͼ�ۼ�����д������
��2���ڣ�1���У�����![]() �����̶�ֱ�����߶�
�����̶�ֱ�����߶�![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ��
��ʹ��![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0���IJ���ͼ���䶥������Ϊ��1��n��������x���һ�������ڵ㣨3��0���ͣ�4��0��֮�䣬�����н��ۣ���4a��2b+c��0����3a+b��0����b2��4a��c��n������һԪ���η���ax2+bx+c��n��1����������ʵ����������ȷ���۵ĸ����ǣ�������
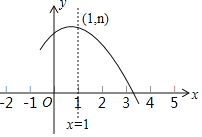
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() �ڵ�һ����ͼ����
�ڵ�һ����ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]()
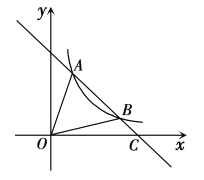
��1�����������Ľ���ʽ��
��2������![]() ��
��![]() ���ϣ���
���ϣ���![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�![]() ��
��![]() ���������۵���ʹ��B���D�غϣ���A�Ķ�Ӧ��Ϊ
���������۵���ʹ��B���D�غϣ���A�Ķ�Ӧ��Ϊ![]() ���ۺ�EF�ij�Ϊ________.
���ۺ�EF�ij�Ϊ________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ѧ������Ȥ���ã�ѧУ���������꼶������Ȥ�࣬��Ȥ���������ࣺ![]() Χ��ࣻ
Χ��ࣻ![]() ����ࣻ
����ࣻ![]() �鷨�ࣻ
�鷨�ࣻ![]() ��Ӱ�࣮Ϊ�˱��ڷְ࣬�꼶���������˲���ѧ����ѡ������ÿ��ѡ��һ�ࣩ������������ͼ��ʾ������ͳ��ͼ�����������������ͼ����Ϣ����������⣺
��Ӱ�࣮Ϊ�˱��ڷְ࣬�꼶���������˲���ѧ����ѡ������ÿ��ѡ��һ�ࣩ������������ͼ��ʾ������ͳ��ͼ�����������������ͼ����Ϣ����������⣺
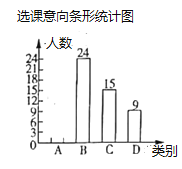
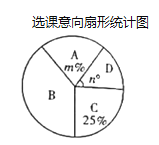
��1��������ͳ��ͼ��![]() ��
��![]() ��ֵ������ȫ����ͳ��ͼ��
��ֵ������ȫ����ͳ��ͼ��
��2����֪��У���꼶��600��ѧ����ѧУ�ƻ�����������Χ��ࡱ��ÿ��Ҫ����40�ˣ�ʵ������ְ࣮
��ѧУ�Ŀ���ƻ��Ƿ�������ѡ��Χ��ࡱ��ѧ����Ը��˵�����ɣ�
��չ����չ����һ��˫��̥�����Ƕ�ѡ���ˡ�Χ��ࡱ������ϣ���ֵܷ�ͬһ���࣬����״ͼ���б��������ǵ�ϣ������ʵ�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���и߶���ͬ��һ�η�ľ��һ��Բľ�����֮����1:1���ڸ߶Ȳ��������£��������ľ�ӹ��ɾ����ܴ��Բ������Բľ�ӹ��ɾ����ܴ�ij����壬��õ���Բ���ͳ���������֮��Ϊ____��
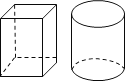
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����y��![]() �ϵĶ��㣬����AO���ӳ���˫�����ڵ�B�����߶�AB��B˳ʱ����ת60��õ��߶�BC����C��˫����y��
�ϵĶ��㣬����AO���ӳ���˫�����ڵ�B�����߶�AB��B˳ʱ����ת60��õ��߶�BC����C��˫����y��![]() �ϵ��˶�����k��____��
�ϵ��˶�����k��____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=ax2+bx+3����A����3��0����B��1��0�����㣬��y�ύ�ڵ�C���䶥��ΪD������AD����P���߶�AD��һ�����㣨����A��D�غϣ�������P��y��Ĵ��ߣ������ΪE������AE��
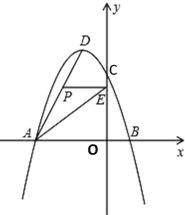
��1���������ߵĺ�������ʽ����д������D�����ꣻ
��2�����P�������Ϊ��x��y������PAE�����ΪS����S��x֮��ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ�������S�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com