
【题目】如图,已知![]() ,
,![]() ,
,![]() 分别是射线
分别是射线![]() ,
,![]() 上的点.
上的点.
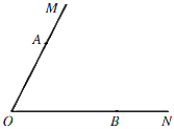
(1)尺规作图:在![]() 的内部确定一点
的内部确定一点![]() ,使得
,使得![]() 且
且![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)在(1)中,连接![]() ,用无刻度直尺在线段
,用无刻度直尺在线段![]() 上确定一点
上确定一点![]() ,使得
,使得![]() ,并证明
,并证明![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
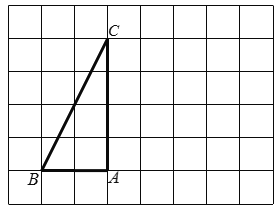
【题目】如图,在每个小正方形的边长为![]() 的网格中,△
的网格中,△![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(1)![]() 的长等于_____________;
的长等于_____________;
(2)在如图所示的网格中,将△![]() 绕点
绕点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,得到△
上,得到△![]() ,请用无刻度的直尺,画出△
,请用无刻度的直尺,画出△![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
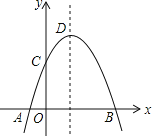
【题目】如图,抛物线y=﹣x2+2x+c+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①抛物线的对称轴是直线x=1;
②若OC=OB,则c=2;
③若M(x0,y0)是x轴上方抛物线上一点,则(x0﹣a)(x0﹣b)<0;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.其中真命题个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
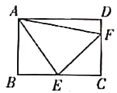
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③![]() .
.
其中正确的是

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
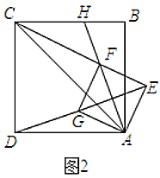
【题目】(1)如图1,正方形![]() 与正方形
与正方形![]() 有公共的顶点
有公共的顶点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
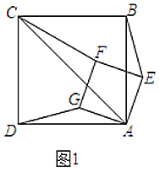
①求证:![]() ;
;
②求![]() 的值;
的值;
(2)将图1中的正方形![]() 旋转到图2的位置,当
旋转到图2的位置,当![]() ,
,![]() ,
,![]() 在一条直线上,若
在一条直线上,若![]() ,求正方形
,求正方形![]() 的边长.
的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 的对称轴是
的对称轴是![]() 轴,过点
轴,过点![]() 作一直线与抛物线
作一直线与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 相交于点
相交于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线![]() 上的任意一点(除顶点外)作该抛物线的切线
上的任意一点(除顶点外)作该抛物线的切线![]() ,分别交直线
,分别交直线![]() 和直线
和直线![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
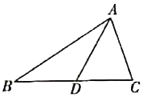
【题目】问题提出
(1)如图,![]() 是
是![]() 的中线,则
的中线,则![]() __________
__________![]() ;(填“
;(填“![]() ”“
”“![]() ”或“
”或“![]() ”)
”)
问题探究
(2)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,当
上任意一点,当![]() 的周长最小时,求
的周长最小时,求![]() 的长;
的长;
问题解决
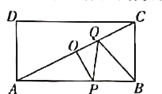
(3)如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,点
的中点,点![]() 为
为![]() 上任意一点,点
上任意一点,点![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,是否存在这样的点
,是否存在这样的点![]() ,使折线
,使折线![]() 的长度最小?若存在,请确定点
的长度最小?若存在,请确定点![]() 的位置,并求出折线
的位置,并求出折线![]() 的最小长度;若不存在,请说明理由.
的最小长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
A.直角三角形B.平行四边形C.菱形D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2020年元月起,收费标准上调为餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2020年处理的这两种垃圾数量与2019年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2019年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2020年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2020年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com