
ΓΨΧβΡΩΓΩ≈ΉΈοœΏyΘΫax2+bx+cΘ®aΓΌ0Θ©”κx÷αΫΜ”ΎΒψAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§2Θ©Θ°
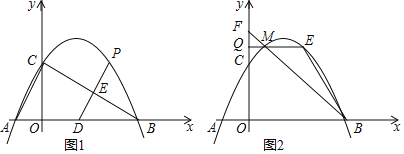
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§ΒψDΒΡΉχ±ξΈΣΘ®2Θ§0Θ©Θ§ΒψP «ΗΟ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”DPΫΜBC”ΎΒψEΘ°Β±ΓςBDE «Β»―ϋ»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ω¥Υ ±ΒψEΒΡΉχ±ξΘΜ
Θ®3Θ©»γΆΦ2Θ§ΒψMΘ®mΘ§nΘ© «≈ΉΈοœΏ…œΈΜ”ΎΕ‘≥Τ÷αΒΡΉσ≤ύ«“≤Μ‘ΎΉχ±ξ÷α…œΒΡΕ·ΒψΘ§ΙΐΒψMΉςx÷αΒΡΤΫ––œΏΫΜy÷α”ΎΒψQΘ§ΫΜ≈ΉΈοœΏ”ΎΝμ“ΜΒψEΘ§÷±œΏBMΫΜy÷α”ΎΒψFΘ§Β±SΓςMFQΘΚSΓςMEBΘΫ1ΘΚ3 ±Θ§«σ≥ωΒψMΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΒψEΒΡΉχ±ξΈΣ
ΘΜΘ®2Θ©ΒψEΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Μρ
Μρ![]() ΘΜΘ®3Θ©ΒψMΒΡΉχ±ξΈΣ
ΘΜΘ®3Θ©ΒψMΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒψ![]() Θ§
Θ§![]() Ήχ±ξ…η≥…≈ΉΈοœΏΫβΈω ΫΘ§‘ΌΫΪΒψ
Ήχ±ξ…η≥…≈ΉΈοœΏΫβΈω ΫΘ§‘ΌΫΪΒψ![]() Ήχ±ξ¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Ήχ±ξ¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©œ»≈–Εœ≥ωΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΘ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
…œΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΘ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©œ»±μ Ψ≥ω![]() Θ§«σ≥ω÷±œΏ
Θ§«σ≥ω÷±œΏ![]() ΒΡΫβΈω ΫΘ§ΒΟ≥ωΒψ
ΒΡΫβΈω ΫΘ§ΒΟ≥ωΒψ![]() ΒΡΉχ±ξΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”Ο
ΒΡΉχ±ξΘ§‘ΌΖ÷»ΐ÷÷«ιΩωΘ§άϊ”Ο![]() Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ§Ϋ®ΝΔΖΫ≥Χ«σΫβΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
ΫβΘΚΘ®1Θ©![]() ≈ΉΈοœΏ
≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§
Θ§
![]() …η≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
![]() ≈ΉΈοœΏ
≈ΉΈοœΏ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©![]() Βψ
Βψ![]() ‘Ύ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§
‘Ύ≈ΉΈοœΏΒΎ“Μœσœό…œΒΡ“ΜΗωΕ·ΒψΘ§
![]() Βψ
Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§
…œΘ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷±œΏ
÷±œΏ
![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]() «Β»―ϋ»ΐΫ«–ΈΘ§
«Β»―ϋ»ΐΫ«–ΈΘ§
![]() Β±
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Βψ
Βψ![]() «
«![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
![]() Βψ
Βψ![]() ΒΡΚαΉχ±ξ3Θ§
ΒΡΚαΉχ±ξ3Θ§
![]() Βψ
Βψ![]() Θ§
Θ§
Φ¥Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Μρ
Μρ![]() ΘΜ
ΘΜ
Θ®3Θ©![]() Θ§
Θ§![]() Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΕ‘≥Τ÷α÷±œΏΈΣ
≈ΉΈοœΏΒΡΕ‘≥Τ÷α÷±œΏΈΣ![]() Θ§
Θ§
![]() ÷αΘ§
÷αΘ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Θ®…α
Θ®…α![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() Μρ
Μρ![]() Θ®…α
Θ®…α![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Φ¥Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() Θ§
Θ§



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ3ΓΝ3’ΐΖΫ–ΈΖΫΗώ÷–Θ§”–3Ηω–Γ’ΐΖΫ–ΈΆΩ≥…ΝΥΚΎ…ΪΘ§Υυ–Έ≥…ΒΡΆΦΑΗ»γΆΦΥυ ΨΘ§ΆΦ÷–ΟΩΩι–Γ’ΐΖΫ–Έ≥ΐ―’…ΪΆβΆξ»ΪœύΆ§Θ°
Θ®1Θ©“ΜΗω–Γ«ρ‘Ύ’βΗω’ΐΖΫ–ΈΖΫΗώ…œΉ‘”…ΙωΕ·Θ§Ρ«Ο¥–Γ«ρΆΘ‘ΎΚΎ…Ϊ–Γ’ΐΖΫ–ΈΒΡΗ≈¬ «Εύ…ΌΘΩ
Θ®2Θ©œ÷ΫΪΖΫΗώΡΎΩ’ΑΉΒΡ–Γ’ΐΖΫ–ΈΘ®AΓΔBΓΔCΓΔDΓΔEΓΔFΘ©÷–»Έ»Γ2ΗωΆΩΚΎΘ§ΒΟΒΫ–¬ΆΦΑΗΘ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®«σ–¬ΆΦΑΗ «÷––ΡΕ‘≥ΤΆΦ–ΈΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ¬ζΉψ―ß…ζΒΡ–Υ»ΛΑ°ΚΟΘ§―ß–ΘΨωΕ®‘ΎΤΏΡξΦΕΩΣ…η–Υ»ΛΑύΘ§–Υ»ΛΑύ…η”–ΥΡάύΘΚ![]() ΈßΤεΑύΘΜ
ΈßΤεΑύΘΜ![]() œσΤεΑύΘΜ
œσΤεΑύΘΜ![]() ιΖ®ΑύΘΜ
ιΖ®ΑύΘΜ![]() …ψ”ΑΑύΘ°ΈΣΝΥ±ψ”ΎΖ÷ΑύΘ§ΡξΦΕΉιΥφΜζ≥ι≤ιΝΥ≤ΩΖ÷―ß…ζΒΡ―ΓΩΈ“βœρΘ®ΟΩ»Υ―Γ±®“ΜάύΘ©Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΝΫΖυΆ≥ΦΤΆΦΘ®≤ΜΆξ’ϊΘ©Θ§«κΗυΨίΆΦ÷––≈œΔΘ§Ϋβ¥πœ¬Έ ΧβΘΚ
…ψ”ΑΑύΘ°ΈΣΝΥ±ψ”ΎΖ÷ΑύΘ§ΡξΦΕΉιΥφΜζ≥ι≤ιΝΥ≤ΩΖ÷―ß…ζΒΡ―ΓΩΈ“βœρΘ®ΟΩ»Υ―Γ±®“ΜάύΘ©Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΝΫΖυΆ≥ΦΤΆΦΘ®≤ΜΆξ’ϊΘ©Θ§«κΗυΨίΆΦ÷––≈œΔΘ§Ϋβ¥πœ¬Έ ΧβΘΚ
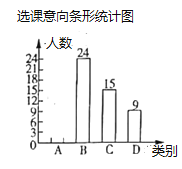
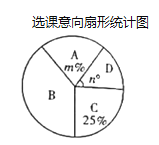
Θ®1Θ©«σ…»–ΈΆ≥ΦΤΆΦ÷–![]() ΓΔ
ΓΔ![]() ΒΡ÷ΒΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
ΒΡ÷ΒΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©“―÷ΣΗΟ–ΘΤΏΡξΦΕ”–600Οϊ―ß…ζΘ§―ß–ΘΦΤΜ°ΩΣ…η»ΐΗωΓΑΈßΤεΑύΓ±Θ§ΟΩΑύ“Σ«σ≤Μ≥§Ιΐ40»ΥΘ§ Β––ΥφΜζΖ÷ΑύΘ°
ΔΌ―ß–ΘΒΡΩΣΑύΦΤΜ° «ΖώΡή¬ζΉψ―Γ‘ώΓΑΈßΤεΑύΓ±ΒΡ―ß…ζ“β‘ΗΘ§ΥΒΟςάμ”…ΘΜ
ΔΎ’Ι≈τΓΔ’ΙΖ… «“ΜΕ‘ΥΪΑϊΧΞΘ§ΥϊΟ«ΕΦ―Γ‘ώΝΥΓΑΈßΤεΑύΓ±Θ§≤Δ«“œΘΆϊΡήΖ÷ΒΫΆ§“ΜΗωΑύΘ§”Ο ςΉ¥ΆΦΜρΝ–±μΖ®«σΥϊΟ«ΒΡœΘΆϊΒΟ“‘ Βœ÷ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Κ”≈‘”–“ΜΉυ–Γ…ΫΘ§¥”…ΫΕΞA¥Π≤βΒΟΚ”Ε‘ΑΕΒψCΒΡΗ©Ϋ«ΈΣ30ΓψΘ§≤βΒΟΑΕ±ΏΒψDΒΡΗ©Ϋ«ΈΣ45ΓψΘ§œ÷¥”…ΫΕΞAΒΫΚ”Ε‘ΑΕΒψCά≠“ΜΧθ± ÷±ΒΡά¬…ΰACΘ§»γΙϊAC «120ΟΉΘ§«σΚ”ΩμCDΒΡ≥ΛΘΩ
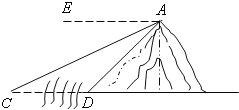
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψA «ΥΪ«ζœΏyΘΫ![]() …œΒΡΕ·ΒψΘ§Ν§ΫαAO≤Δ―”≥ΛΫΜΥΪ«ζœΏ”ΎΒψBΘ§ΫΪœΏΕΈAB»ΤBΥ≥ ±’κ–ΐΉΣ60ΓψΒΟΒΫœΏΕΈBCΘ§ΒψC‘ΎΥΪ«ζœΏyΘΫ
…œΒΡΕ·ΒψΘ§Ν§ΫαAO≤Δ―”≥ΛΫΜΥΪ«ζœΏ”ΎΒψBΘ§ΫΪœΏΕΈAB»ΤBΥ≥ ±’κ–ΐΉΣ60ΓψΒΟΒΫœΏΕΈBCΘ§ΒψC‘ΎΥΪ«ζœΏyΘΫ![]() …œΒΡ‘ΥΕ·Θ§‘ρkΘΫ____Θ°
…œΒΡ‘ΥΕ·Θ§‘ρkΘΫ____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§”κΖ¥±»άΐΚ· ΐ
Θ§”κΖ¥±»άΐΚ· ΐ![]() ‘ΎΒΎΕΰœσœόΡΎΒΡΆΦœσœύΫΜ”ΎΒψ
‘ΎΒΎΕΰœσœόΡΎΒΡΆΦœσœύΫΜ”ΎΒψ![]() Θ°
Θ°
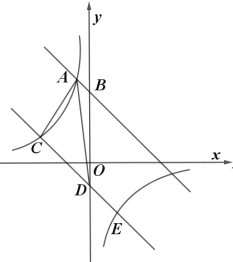
![]() «σ÷±œΏ
«σ÷±œΏ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
![]() ΫΪ÷±œΏ
ΫΪ÷±œΏ![]() œρœ¬ΤΫ“Τ
œρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜΚσ”κΖ¥±»άΐΚ· ΐΒΡΆΦœσΫΜ”ΎΒψ
ΗωΒΞΈΜΚσ”κΖ¥±»άΐΚ· ΐΒΡΆΦœσΫΜ”ΎΒψ![]() ΚΆΒψ
ΚΆΒψ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() «σ
«σ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§Ψ≠Ιΐ
Θ§Ψ≠Ιΐ![]() ΓΔ
ΓΔ![]() ΝΫΒψΒΡ≈ΉΈοœΏ
ΝΫΒψΒΡ≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΒΡΝμ“ΜΫΜΒψ
÷αΒΡΝμ“ΜΫΜΒψ![]() Θ°
Θ°
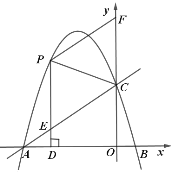
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©![]() «ΗΟ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ§ΙΐΒψ
«ΗΟ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ°
Θ°
ΔΌ«σ≥ωΥΡ±Ώ–Έ![]() ΒΡ÷ή≥Λ
ΒΡ÷ή≥Λ![]() ”κ
”κ![]() ΒΡΚ· ΐ±μ¥ο ΫΘ§≤Δ«σ
ΒΡΚ· ΐ±μ¥ο ΫΘ§≤Δ«σ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
ΔΎΒ±![]() ΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–Έ
ΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–Έ![]() «Νβ–ΈΘΜ
«Νβ–ΈΘΜ
Δέ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ“‘
Θ§ ΙΒΟ“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ![]() œύΥΤΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω¬ζΉψΧθΦΰΒΡΒψ
œύΥΤΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω¬ζΉψΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥”Έά÷‘Α”–“ΜΗω÷±ΨΕΈΣ16ΟΉΒΡ‘≤–Έ≈γΥ°≥ΊΘ§≈γΥ°≥ΊΒΡ÷ή±Ώ”–“Μ»Π≈γΥ°ΆΖΘ§≈γ≥ωΒΡΥ°÷υΈΣ≈ΉΈοœΏΘ§‘ΎΨύΥ°≥Ί÷––Ρ3ΟΉ¥Π¥οΒΫΉνΗΏΘ§ΗΏΕ»ΈΣ5ΟΉΘ§«“ΗςΖΫœρ≈γ≥ωΒΡΥ°÷υ«ΓΚΟ‘Ύ≈γΥ°≥Ί÷––ΡΒΡΉΑ ΈΈο¥ΠΜψΚœΘ°»γΆΦΥυ ΨΘ§“‘Υ°ΤΫΖΫœρΈΣx÷αΘ§≈γΥ°≥Ί÷––ΡΈΣ‘≠ΒψΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒΘ°
Θ®1Θ©«σΥ°÷υΥυ‘Ύ≈ΉΈοœΏΘ®ΒΎ“Μœσœό≤ΩΖ÷Θ©ΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©Άθ ΠΗΒ‘Ύ≈γΥ°≥ΊΡΎΈ§–ό…η±ΗΤΎΦδΘ§≈γΥ°Ιή“βΆβ≈γΥ°Θ§ΈΣΝΥ≤Μ±ΜΝή ΣΘ§…μΗΏ1.8ΟΉΒΡΆθ ΠΗΒ’ΨΝΔ ±±Ί–κ‘ΎάκΥ°≥Ί÷––ΡΕύ…ΌΟΉ“‘ΡΎΘΩ
Θ®3Θ©Ψ≠Φλ–όΤάΙάΘ§”Έά÷‘ΑΨωΕ®Ε‘≈γΥ°…η ©Ήω»γœ¬…ηΦΤΗΡΫχΘΚ‘Ύ≈γ≥ωΥ°÷υΒΡ–ΈΉ¥≤Μ±δΒΡ«ΑΧαœ¬Θ§Α―Υ°≥ΊΒΡ÷±ΨΕά©¥σΒΫ32ΟΉΘ§ΗςΖΫœρ≈γ≥ωΒΡΥ°÷υ»‘‘Ύ≈γΥ°≥Ί÷––Ρ±ΘΝτΒΡ‘≠ΉΑ ΈΈοΘ®ΗΏΕ»≤Μ±δΘ©¥ΠΜψΚœΘ§«κΧΫΨΩά©Ϋ®ΗΡ‘λΚσ≈γΥ°≥ΊΥ°÷υΒΡΉν¥σΗΏΕ»Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”Ύ“ΜΗωΚ· ΐΘ§Ή‘±δΝΩx»Γa ±Θ§Κ· ΐ÷Βy“≤Β»”ΎaΘ§Έ“Ο«≥ΤaΈΣ’βΗωΚ· ΐΒΡ≤ΜΕ·Βψ.»γΙϊΕΰ¥ΈΚ· ΐyΘΫx2+2x+c”–ΝΫΗωœύ“λΒΡ≤ΜΕ·Βψx1ΓΔx2Θ§«“x1ΘΦ1ΘΦx2Θ§‘ρcΒΡ»Γ÷ΒΖΕΈß «( )
A. cΘΦ©¹3B. cΘΦ©¹2C. cΘΦ![]() D. cΘΦ1
D. cΘΦ1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com