
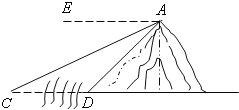
【题目】如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长?
【答案】60![]() -60
-60
【解析】
首先过点A作AF⊥CD于F,由题意可知∠ACF=30°,∠ADF=45°,AC=120,在Rt△ACF与Rt△ADF中,利用三角函数值,即可求得CF与DF的长,然后由CD=CF-DF,即可求得河宽CD的长.
解:过点A作AF⊥CD于F,
根据题意知∠ACF=30°,∠ADF=![]() ,AC=120,
,AC=120,
在Rt△ACF中,cos∠ACF=![]() =cos30°=
=cos30°=![]() ,
,
∴CF=120×![]() =60
=60![]() ,
,
又sin∠ACF=![]() =sin30°=
=sin30°=![]() ,∴AF=120×
,∴AF=120×![]() =60,
=60,
在Rt△ADF中,tan∠ADF=![]() = tan45°=1,
= tan45°=1,
∴DF=60,∴CD=CF-DF=60![]() -60,
-60,
答:河宽CD的长为(60![]() -60)米.
-60)米.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
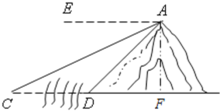
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月22日14时30分,全球新冠肺炎确诊病例达305740例,超过30万,死亡病例累计12762人,将“305740”这个数字用科学记数法表示保留两位有效数字为( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
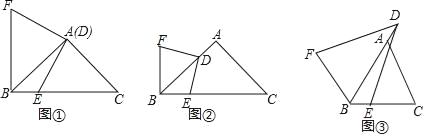
【题目】观察猜想:(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是 ,BE+BF= ;
探究证明:(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;
拓展延伸:(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.
(1)用含x的代数式表示:第一次购进手链的数量为 条;
(2)求x的值;
(3)不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
(1)求点D的坐标和直线BC对应的一次函数关系式;
(2)若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;
(3)如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.
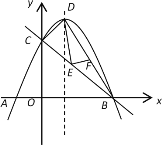
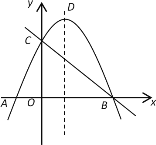
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2).
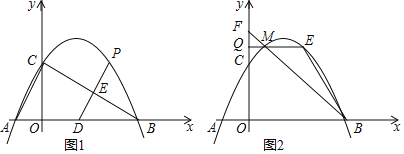
(1)求抛物线的解析式;
(2)如图1,点D的坐标为(2,0),点P是该抛物线第一象限上的一个动点,连接DP交BC于点E.当△BDE是等腰三角形时,直接写出此时点E的坐标;
(3)如图2,点M(m,n)是抛物线上位于对称轴的左侧且不在坐标轴上的动点,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F,当S△MFQ:S△MEB=1:3时,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒席卷全球,疫情当前,全国上下砥砺同行.某中学校指导中心为引导未成年人以健康心理、阳光心态抗击疫情,积极开展了心理援助工作,并推出“你是我的奥特曼”有奖征稿活动.活动结束后,该指导中心对参赛学生的获奖情况进行统计,并绘制了如下两幅不完整的统计图.
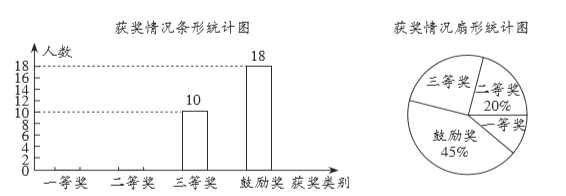
结合图中的相关数据,解答下列问题:
(1)参加此次有奖征稿活动的学生有 人,在扇形统计图中,“三等奖”所对应扇形的圆心角度数为 ;
(2)将条形统计图补充完整;
(3)若获得“一等奖”的学生中有![]() 来自七年级,
来自七年级,![]() 来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
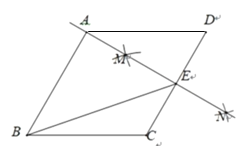
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com