
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
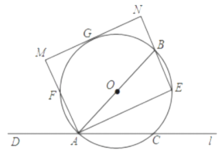
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①13;②![]()
【解析】
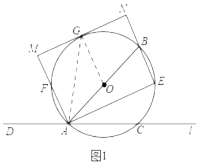
(1)如图1,连接GO、GA,先根据角平分线的定义证明∠MAE=![]() (∠BAC+∠BAD)=90°,由圆周角定理和同圆的半径相等得∠OGA=∠FAG,则OG∥AM,所以∠MGO=180-∠M=90,从而得结论;
(∠BAC+∠BAD)=90°,由圆周角定理和同圆的半径相等得∠OGA=∠FAG,则OG∥AM,所以∠MGO=180-∠M=90,从而得结论;
(2)①延长GO交AE于点P,证明四边形MGPA为矩形,得GP=MA=18,∠GPA=90°,设OA=OG=r,则OP=18-r,根据勾股定理列方程解出即可;
②如图3,过M作MH⊥l,连接BC,延长NE交l于I,连接GO交延长交AE于P,tan∠MAH=tan∠ABE=tan∠BIA=![]() ,BI=2BE=20,根据三角函数计算MH,AH,CI的长,最后计算MH和HC的长,代入tan∠MCD=
,BI=2BE=20,根据三角函数计算MH,AH,CI的长,最后计算MH和HC的长,代入tan∠MCD=![]() ,可得结论.
,可得结论.
(1)证明:如图1,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 半径,
半径,
∴![]() 是
是![]() 的切线.
的切线.
(2)解:①如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,

∵![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,即
,即![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
故![]() 的半径是13.
的半径是13.
②如图3,过![]() 作
作![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ,
,
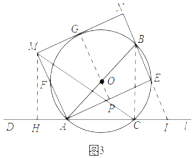
由①知:![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() 上的动点,连结AO并延长交双曲线于点B,将线段AB绕B顺时针旋转60°得到线段BC,点C在双曲线y=
上的动点,连结AO并延长交双曲线于点B,将线段AB绕B顺时针旋转60°得到线段BC,点C在双曲线y=![]() 上的运动,则k=____.
上的运动,则k=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0),B(1,0)两点,与y轴交于点C,其顶点为D,连接AD,点P是线段AD上一个动点(不与A,D重合),过点P作y轴的垂线,垂足点为E,连接AE.
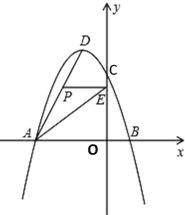
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
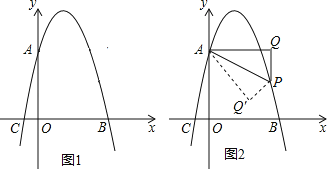
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.机场对乘客进行安检不能采用抽样调查
B.一组数据10,11,12,9,8的平均数是10,方差是2
C.“清明时节雨纷纷”是随机事件
D.一组数据6,5,3,5,4的众数是5,中位数是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出):有同样大小正方形256个,拼成如图1所示的![]() 的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?
的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?

(问题探究):我们先考虑以下简单的情况:一条直线穿越一个正方形的情况.(如图2)
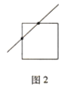
从图中我们可以看出,当一条直线穿过一个小正方形时,这条直线最多与正方形上、下、左、右四条边中的两个边相交,所以当一条直线穿过一个小正方形时,这条直线会与其中某两条边产生两个交点,并且以两个交点为顶点的线段会全部落在小正方形内.
这就启发我们:为了求出直线![]() 最多穿过多少个小正方形,我们可以转而去考虑当直线
最多穿过多少个小正方形,我们可以转而去考虑当直线![]() 穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
再让我们来考虑![]() 正方形的情况(如图3):
正方形的情况(如图3):
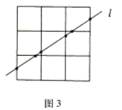
为了让直线穿越更多的小正方形,我们不妨假设直线![]() 右上方至左下方穿过一个
右上方至左下方穿过一个![]() 的正方形,我们从两个方向来分析直线
的正方形,我们从两个方向来分析直线![]() 穿过
穿过![]() 正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线
正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线![]() 最多可穿过
最多可穿过![]() 的大正方形中的六条线段,从而直线
的大正方形中的六条线段,从而直线![]() 上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线
上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线![]() 最多能经过5个小正方形.
最多能经过5个小正方形.
(问题解决):
(1)有同样大小的小正方形16个,拼成如图4所示的![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.

(2)有同样大小的小正方形256个,拼成![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
(3)如果用一条直线穿过![]() 的大正方形的话,最多可以穿过___________个小正方形.
的大正方形的话,最多可以穿过___________个小正方形.
(问题拓展):
(4)如果用一条直线穿过![]() 的大长方形的话(如图5),最多可以穿过个___________小正方形.
的大长方形的话(如图5),最多可以穿过个___________小正方形.

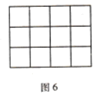
(5)如果用一条直线穿过![]() 的大长方形的话(如图6),最多可以穿过___________个小正方形.
的大长方形的话(如图6),最多可以穿过___________个小正方形.
(6)如果用一条直线穿过![]() 的大长方形的话,最多可以穿过________个小正方形.
的大长方形的话,最多可以穿过________个小正方形.
(类比探究):
由二维的平面我们可以联想到三维的立体空间,平面中的正方形中四条边可联想到正方体中的正方形的六个面,类比上面问题解决的方法解决如下问题:
(7)如图7有同样大小的小正方体8个,拼成如图所示的![]() 的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
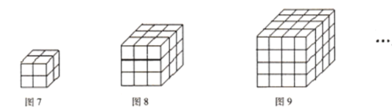
(8)如果用一条直线穿过![]() 的大正方体的话,最多可以穿过_________个小正方体.
的大正方体的话,最多可以穿过_________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
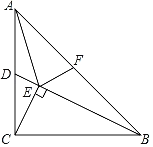
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=2,D是边AC的中点,CE⊥BD于E.若F是边AB上的点,且使△AEF为等腰三角形,则AF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com