
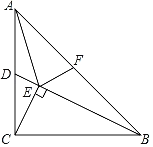
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=2,D是边AC的中点,CE⊥BD于E.若F是边AB上的点,且使△AEF为等腰三角形,则AF的长为_____.
【答案】![]() 或
或![]() 或
或![]()
【解析】
由相似三角形的性质可求AH的长,BH的长,分三种情况讨论,由等腰三角形的性质和勾股定理可求解.
解:∵∠ACB=90°,AC=BC=2,
∴AB=![]()
∵∠DCB=90°,CE⊥BD,
∴△CDE∽△BDC,
∴CD2=DEDB,
∵AD=CD,
∴AD2=DEDB,
∴![]() ,
,
∵∠ADE∠ADB,
△DAE∽△DBA;
∴![]() ,
,
∴AE=![]() ,
,
∵DE=![]() ,BD=
,BD=![]() ,
,
∴BE=![]() ,
,
如图1中,若AE=AF时,
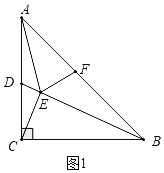
∴AF=![]() ;
;
如图2中,若FE=AE时,过点E作EJ⊥AB于J,
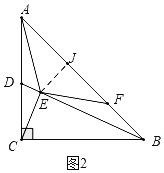
∵JE2=AE2﹣AJ2=EB2﹣BJ2,
∴![]() ﹣AJ2=
﹣AJ2=![]() ﹣(2
﹣(2![]() ﹣AJ)2,
﹣AJ)2,
∴AJ=![]() ,
,
∵AE=EF,EJ⊥AF,
∴AF=2AJ=![]() ,
,
如图3中,若EF=AF时,过点E作EJ⊥AB于J,
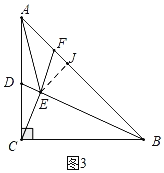
∵EJ2=AE2﹣AJ2=EF2﹣FJ2,
∴![]() ﹣
﹣![]() =AF2﹣(
=AF2﹣(![]() ﹣AF)2,
﹣AF)2,
∴AF=![]() ,
,
综上所述:AD的长为![]() 或
或![]() 或
或![]() .
.
故答案为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
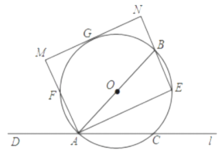
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
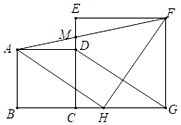
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学校旗杆AB旁边有一个半侧的时钟模型,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2m,旗杆的底端A到钟面9点刻度C的距离为11m,一天小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1米长的标杆的影长1.2m.求旗杆AB的高度.
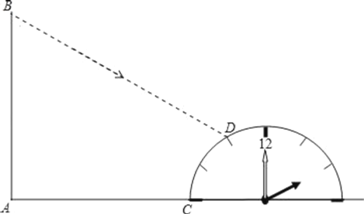
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
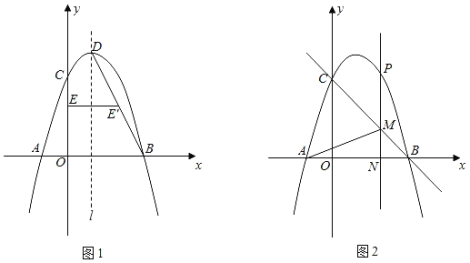
【题目】如图1,二次函数y=﹣x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l是抛物线的对称轴,D是抛物线的顶点.
(1)求该抛物线的函数表达式;
(2)如图1,连结BD,线段OC上点E关于直线l的对称点E'恰好在线段BD上,求点E的坐标;
(3)如图2,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线分别与BC交于点M,与x轴交于点N.试问:抛物线上是否存在点Q,使得△PQN与△AMN的面积相等,且线段PQ的长度最小?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,工匠师傅在板材边角处作直角时,往往使用“三弧法”,作法如下:
(1)作线段![]() ,分别以
,分别以![]() 为圆心,以
为圆心,以![]() 长为半径作弧,两弧的交点为
长为半径作弧,两弧的交点为![]() ;
;
(2)以![]() 为圆心,仍以
为圆心,仍以![]() 长为半径作弧交
长为半径作弧交![]() 的延长线于点
的延长线于点![]()
(3)连接![]() 下列说法中,不正确的是( )
下列说法中,不正确的是( )
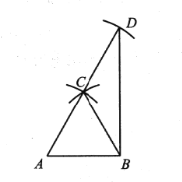
A.![]() 是正三角形B.点
是正三角形B.点![]() 是
是![]() 的外心
的外心
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,双曲线
,双曲线![]() 经过点
经过点![]() .
.

(1)求直线![]() 和双曲线
和双曲线![]() 的解析式.
的解析式.
(2)平移直线![]() ,使它与双曲线
,使它与双曲线![]() 有唯一公共点
有唯一公共点![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com