
����Ŀ��ijҩƷ�������ع���5�������ߣ�ÿ��������ÿ������ҩƷ20��У��û��ش���ӵ�һ���¿�ʼ��������½�������ÿ�������߽����������죮����ʱ��ÿ����ֻ��������һ�������ߣ����������ߵ���ͣ���������¸���Ͷ�����������������������������������飬ÿ�����������������ÿ�µIJ������ԭ�����20%��
��1���������⣬����������⣺
�ٰ��±�����������ֱ��д�ں����ϣ���
���� | ��1���� | ��2���� | ��3���� | ��4���� | ��5���� | ��6���� | �� |
����/��� | �� �� | �� �� | �� �� | 92 | �� | �� | �� |
�ڴӵ�1���½�������������� �����µIJ�����ʼ����δ��������ʱ�IJ�����
��2�����û��ص�x���£�1��x��5����x���������IJ���Ϊy��У���y����x�ĺ�����ϵʽ��
��3����֪ÿ�������ߵ������������30��Ԫ��ÿ��ҩƷ�ɻ���3Ԫ����ӵ�1���¿�ʼ�������������ҩƷ����������ΪW1��Ԫ��ͬʱ���ڣ���������������������ΪW2��Ԫ�����ٵ���n���£�nΪ��������ʱ��W1����W2����n��ֵ����������������ѣ�
���𰸡���1����80��84��88����6����2��y��4x+76��1��x��5����x������������3��nΪ11
��������
��1���ٸ����������д��ǰ�����µIJ������Ӷ����Խ���⣻
�ڸ����������д����5��Ԫ�͵�6���µIJ������Ӷ����Խ���⣻
��2�������������д��y����x�ĺ�����ϵʽ��
��3������������Ա�ʾ��W1����W2���Ӷ����Եõ�n��ֵ��
�⣺��1����������ɵã�
��1���µIJ����ǣ�20��4��80��
��2���µIJ����ǣ�20��3+20��1+20%����84��
��3���µIJ����ǣ�20��2+20��1+20%����2��88��
�ʴ�Ϊ��80��84��88��
��������ɵã�
��5���µIJ����ǣ�20��1+20%����4��96��
��6���µIJ����ǣ�20��1+20%����5��120��
�ʴ�Ϊ��6��
��2��������ɵ�
y��20����5��1��+20��20%��x��1����4x+76��
��y��x�ĺ�����ϵʽΪy��4x+76��![]() ����x����������
����x����������
��3���ɣ�1���ڿ�֪��������6���µIJ�����������������²���������ǰ5�����ڼ�W1<W2
�߸����ǰ5���µ��ܲ�����80+84+88+92+96��440����У�
�൱n��6ʱ��
W1��440��3+��n��5����20����1+20%����5��3��30��5��360n��630��
W2��20��5��3��n��300n��
��W1>W2ʱ����360n��630>330n�����n>10.5��
��n��������
��nΪ11��


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
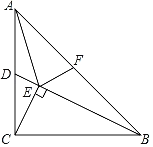
����Ŀ����ͼ������ABC�У���ACB��90����AC��BC��2��D�DZ�AC���е㣬CE��BD��E����F�DZ�AB�ϵĵ㣬��ʹ��AEFΪ���������Σ���AF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ��������ҵ糧���ڹ���ж����ƣ����ǵ�ij�ֵ��Ӳ�Ʒ����������µ�ʹ����������![]() �꣬��������ⲿ�Ŷ����������۵IJ�Ʒ��ʹ���������и��ٵ��飬ͳ�ƽ�����£�����λ���꣩
�꣬��������ⲿ�Ŷ����������۵IJ�Ʒ��ʹ���������и��ٵ��飬ͳ�ƽ�����£�����λ���꣩
�׳���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�ҳ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��ش��������⣺
��1����գ�
ƽ���� | ���� | ��λ�� | |
�׳� | _____ |
|
|
�ҳ� |
| ______ |
|
���� |
|
| ______ |
��2�����������ҵ����۹��ֱ���������һ�ֱ�ʾ�������Ƶ���������
��3��������ǹ˿ͣ��������������һ�ҵĵ��Ӳ�Ʒ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ��AOB�ı�OA��һ�㣬OC=6��NΪ��OB�����ڵ�O��һ���㣬P���߶�CN��һ�㣬����P�ֱ���PQ��OA��OB�ڵ�Q��PM��OB��OA�ڵ�M��
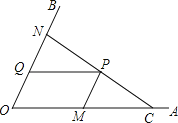
��1������AOB=45�㣬OM=4��OQ=![]() ����֤��CN��OB��
����֤��CN��OB��
��2������N�ڱ�OB���˶�ʱ���ı���OMPQʼ�ձ���Ϊ���Σ�
���ʣ�![]() ��ֵ�Ƿ����仯������仯�������ȡֵ��Χ��������䣬��˵�����ɣ�
��ֵ�Ƿ����仯������仯�������ȡֵ��Χ��������䣬��˵�����ɣ�
��������OMPQ�����ΪS1����NOC�����ΪS2����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
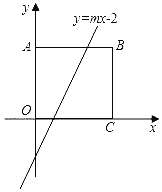
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCO�������Σ���B������Ϊ(4��4)��
��1��ֱ��y��mx��2ǡ�ð�������ABCO������ֳ���ȵ������֣���m��_____��
��2����ֱ��y��mx��2��������ABCO�ı������������㣬��m��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
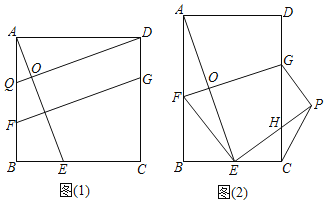
����Ŀ����1��֤���ƶϣ���ͼ��1������������![]() �У���
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��
����֤��![]() ��
��
���ƶϣ�![]() ��ֵΪ�� ����
��ֵΪ�� ����
��2�����̽������ͼ��2�����ھ���![]() �У�
��![]() ��
��![]() ��������������
��������������![]() ��
��![]() �۵���ʹ��
�۵���ʹ��![]() ����
����![]() ���ϵĵ�
���ϵĵ�![]() �����õ��ı���
�����õ��ı���![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����̽��
����̽��![]() ��
��![]() CP֮���������ϵ����˵�����ɣ�
CP֮���������ϵ����˵�����ɣ�
��3����չӦ�ã��ڣ�2���������£�����![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
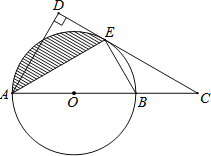
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��AB�ӳ�����һ�㣬CD���O�����ڵ�E��AD��CD�ڵ�D��
��1����֤��AEƽ�֡�DAC��
��2����AB=4����ABE=60�㣬���ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
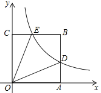
����Ŀ��ƽ��ֱ������ϵ�У�������OABC��ͼ���ã�����������![]() ��ͼ��AB�ڵ�D����BC�ڵ�E����֪A��
��ͼ��AB�ڵ�D����BC�ڵ�E����֪A��![]() ��0������DOE=30������k��ֵΪ�� ��
��0������DOE=30������k��ֵΪ�� ��
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ����֪�ִ�����A���ر�ƫ��65��ķ������ٺ��У�ͬʱ�ִ������ִ�����ƫ��40�㷽��ĵ�B����ijһ�����У��ٶ�����ִ����ٶ���ͬ��������һ��ʱ��������ִ�ǡ�����������ִ��ҵĺ��з���Ϊ��������
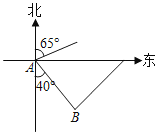
A.��ƫ��40��B.��ƫ��40��C.��ƫ��35��D.��ƫ��35��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com