
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出图中阴影部分的面积.
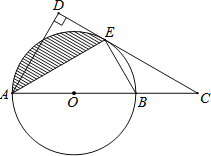
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OE,可证得OE∥AD,则∠DAE=∠AEO=∠EAO,可得结论;
(2)由条件求得∠AOE=120°,容易求得△AOE和扇形AOE的面积,利用面积差可求得阴影部分的面积.
试题解析:(1)证明:连接OE,如图,
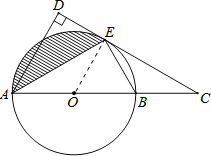
∵CD与⊙O相切于点E,
∴OE⊥CD,
∵AD⊥CD,
∴OE∥AD,
∴∠DAE=∠AEO,
∵AO=OE,
∴∠AEO=∠OAE,
∴∠OAE=∠DAE,
∴AE平分∠DAC;
(2)∵OA=OB,
∴∠AEO=∠OAE=30°,
∴∠AOE=120°,
∴阴影部分的面积=S扇形AOE﹣S△AOE
=S扇形AOE﹣![]() S△ABE
S△ABE
=![]()
=![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1和S2,比较S1与S2的大小( )
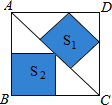
A. S1>S2 B. S1=S2 C. S1<S2 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为某封闭图形边界的一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( ).
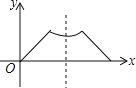
A. 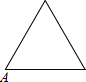 B.
B.  C.
C. 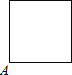 D.
D. 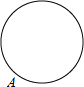
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
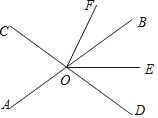
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(x,y)先向左平移4个单位,再向上平移3个单位后得到点P′(1,2),则点P的坐标为( )
A.(2,6)B.(﹣3,5)C.(﹣3,1)D.(5,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com