
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

【答案】(1)存在△MCN与△ODM相似,证明见矩形;
(2)R=![]() ;
;
(3)△CMN的周长是一个定值,理由见解析.
【解析】试题分析:(1)根据切线的性质得出∠OMN=90,从而证得∠OMD=∠MNC;则△ODM∽△MCN;
(2)由DM=x,设OA=OM=R;则得出OD,由勾股定理得R与x的关系;
(3)可分为两种解法得出答案.由△ODM∽△MCN,得![]() ,用含x的式子表示出CN,MN,从而得出△CMN的周长是一个定值.
,用含x的式子表示出CN,MN,从而得出△CMN的周长是一个定值.
试题解析:(1)存在△MCN与△ODM相似,证明如下:
∵MN切⊙O于点M,∴∠OMN=90°,∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°,∴∠OMD=∠MNC,又∵∠D=∠C=90°,∴△ODM∽△MCN.
(2)在Rt△ODM中,DM=x,设OA=OM=R,∴OD=AD﹣OA=8﹣R,由勾股定理得:(8﹣R)2+x2=R2,
∴64﹣16R+R2+x2=R2,∴R=![]() .
.
(3)∵CM=CD﹣DM=8﹣x,OD=8﹣R=8﹣![]() ,且有△ODM∽△MCN,∴
,且有△ODM∽△MCN,∴![]() ,∴代入得到:CN=
,∴代入得到:CN=![]() .
.
同理![]() ,∴代入得到:MN=
,∴代入得到:MN=![]() ,∴△CMN的周长=CM+CN+MN=(8﹣x)+
,∴△CMN的周长=CM+CN+MN=(8﹣x)+![]() +
+![]() =(8﹣x)+(x+8)=16,
=(8﹣x)+(x+8)=16,
在点O的运动过程中,△CMN的周长始终为16,是一个定值.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y1=2x与双曲线y2= ![]() 的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 .
的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
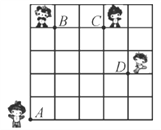
【题目】如图,奥运福娃在5×5的方格(每小格边长为1 m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其他福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A·B(+1,+4),从B到A记为:B·A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A·C(__________,__________),B·C(__________,__________),C·__________(-3,-4);
(2)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出妮妮的位置点E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:
年,德国数学家格奥尔格康托尔引入位于一条线段上的一些点的集合,他的做法如下:
取一条长度为![]() 的线段,将它三等分,去掉中间一段,余下两条线段,达到第
的线段,将它三等分,去掉中间一段,余下两条线段,达到第![]() 阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第
阶段;将剩下的两条线段再分别三等分.各去掉中间一段,余下四条线段,达到第![]() 阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第
阶段;再将剩下的四条线段,分别三等分,各去掉中间一段,余下八条线段,达到第![]() 线段;
线段; ![]() ;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到
;这样的操作一直继续下去,在不断分割舍弃的过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到![]() 个阶段时(
个阶段时(![]() 为正整数),的线段的长度之和为__________.
为正整数),的线段的长度之和为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
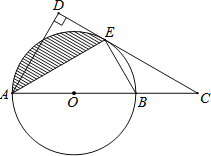
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月17日北京国际自行车大会召开,来自世界各地的4000多名骑游爱好者齐聚夏都延庆.各种自行车赛事也带动了延庆的骑游产业.据调查,延庆区某骑游公司每月的租赁自行车数的增长率相同,今年四月份的骑游人数约为9000人,六月份的骑游人数约为16000人,求该骑游公司租赁自行车数的月平均增长率(精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com