
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是![]() 年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
乙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
丙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
请回答下面问题:
(1)填空:
平均数 | 众数 | 中位数 | |
甲厂 | _____ |
|
|
乙厂 |
| ______ |
|
丙厂 |
|
| ______ |
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
【答案】(1)8;8 ;8;(2)甲厂选用平均数8;乙厂选用众数8;丙厂选用中位数8;(3)宜选购乙厂的产品,理由见解析.
【解析】
(1)平均数就是把这组数据加起来的和除以这组数据的总数,众数就是一堆数中出现次数最多的数,中位数,就是一组数按从小到大的顺序排列,中间位置的那个数,如果有偶数个数,那就是中间的两个数的平均数;
(2)一组数据的平均数、众数、中位数从不同角度表示这种数据集中趋势.由(1)的结果容易回答(2),甲厂、乙厂、丙厂,分别利用了平均数、众数、中位数进行广告推销,顾客在选购产品时,一般以平均数为依据.
(3)根据平均数大的进行选择.
解:(1)甲厂:平均数为![]() (4+5+5+5+5+7+9+12+13+15)=8
(4+5+5+5+5+7+9+12+13+15)=8
乙厂:众数为8,
丙厂:中位数为(7+9)÷2=8.
(2)甲家的销售广告利用了平均数8表示集中趋势的特征数;
乙家的销售广告利用了众数8表示集中趋势的特征数;
丙家的销售广告利用了中位数8表示集中趋势的特征数.
(3)宜选购乙厂的产品,因为乙厂产品平均使用寿命最长且多数超过8年或达到8年寿命.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
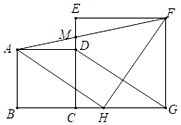
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,工匠师傅在板材边角处作直角时,往往使用“三弧法”,作法如下:
(1)作线段![]() ,分别以
,分别以![]() 为圆心,以
为圆心,以![]() 长为半径作弧,两弧的交点为
长为半径作弧,两弧的交点为![]() ;
;
(2)以![]() 为圆心,仍以
为圆心,仍以![]() 长为半径作弧交
长为半径作弧交![]() 的延长线于点
的延长线于点![]()
(3)连接![]() 下列说法中,不正确的是( )
下列说法中,不正确的是( )
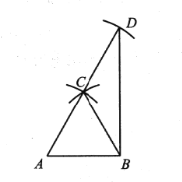
A.![]() 是正三角形B.点
是正三角形B.点![]() 是
是![]() 的外心
的外心
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,双曲线
,双曲线![]() 经过点
经过点![]() .
.

(1)求直线![]() 和双曲线
和双曲线![]() 的解析式.
的解析式.
(2)平移直线![]() ,使它与双曲线
,使它与双曲线![]() 有唯一公共点
有唯一公共点![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
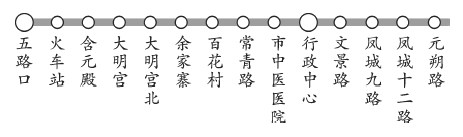
【题目】西安地铁的开通运行给市民的出行方式带来了一些变化,乐乐和小敏利用寒假时间,以问卷的方式对西安市民认为地铁站存在的问题进行调查,如图是西安地铁四号线图(部分).乐乐和小敏分别从行政中心(用![]() 表示)、文景路(用
表示)、文景路(用![]() 表示)、凤城九路(用
表示)、凤城九路(用![]() 表示)这三站中,随机选取一站作为调查的站点.
表示)这三站中,随机选取一站作为调查的站点.
(1)在这三站中,求乐乐选取问卷调查的站点是文景路站的概率;
(2)请你用画树状图或列表法,求乐乐和小敏所选取问卷调查的站点相邻的概率.(各站点用相应的字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )

A.20海里 B.40海里 C.![]() 海里 D.
海里 D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线![]() 于点E.
于点E.
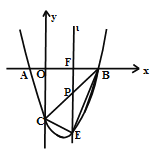
(1)求A、B、C三点的坐标;
(2)当点P在线段BC上运动时,求线段PE长的最大值;
(3)当PE取最大值时,把抛物线![]() 向右平移得到抛物线
向右平移得到抛物线![]() ,抛物线
,抛物线![]() 与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线
与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线![]() 应向右平移几个单位长度可得到抛物线
应向右平移几个单位长度可得到抛物线![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com