
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,斜边
,斜边![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为圆心,线段
为圆心,线段![]() 的长为半径画圆心角为
的长为半径画圆心角为![]() 的扇形
的扇形![]() ,弧
,弧![]() 经过点
经过点![]() ,则图中阴影部分的面积为_______平方单位.
,则图中阴影部分的面积为_______平方单位.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ、DP交于点O,并分别与边CD、BC交于点F、E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD<S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的是_____.(请将正确结论的序号填写在横线上)
,其中正确结论的是_____.(请将正确结论的序号填写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为![]() ,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量
,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (单位:千克)与销售单价
(单位:千克)与销售单价![]() (单位:
(单位: ![]() )之间的函数关系如图
)之间的函数关系如图
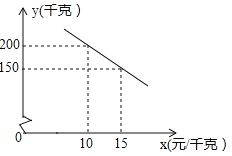
(1)求![]() 与
与![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大,最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是![]() 年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
乙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
丙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
请回答下面问题:
(1)填空:
平均数 | 众数 | 中位数 | |
甲厂 | _____ |
|
|
乙厂 |
| ______ |
|
丙厂 |
|
| ______ |
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2018郑州模拟)如图,抛物线![]() 过点
过点![]() ,与y轴交于点C.
,与y轴交于点C.
(1)求该抛物线的解析式;
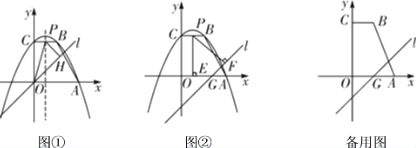
(2)如图①,直线l的解析式为![]() ,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求
,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求![]() 的面积;
的面积;
(3)把图①中的直线![]() 向下平移4个单位长度得到直线
向下平移4个单位长度得到直线![]() ,如图②,直线
,如图②,直线![]() 与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E、F.是否存在点P,使得以P、E、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E、F.是否存在点P,使得以P、E、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
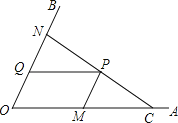
(1)若∠AOB=45°,OM=4,OQ=![]() ,求证:CN⊥OB;
,求证:CN⊥OB;
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
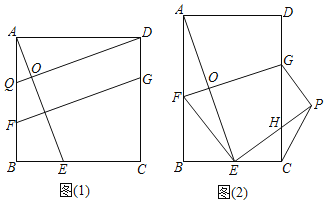
【题目】(1)证明推断:如图(1),在正方形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() 于点
于点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() .
.
①求证:![]() ;
;
②推断:![]() 的值为 ;
的值为 ;
(2)类比探究:如图(2),在矩形![]() 中,
中,![]() (
(![]() 为常数).将矩形
为常数).将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .试探究
.试探究![]() 与
与![]() CP之间的数量关系,并说明理由;
CP之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接![]() ,当
,当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
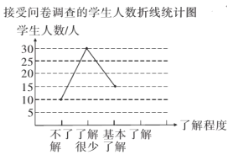
【题目】我校准备近期做一个关于新冠肺炎的专刊学生手抄报,想知道同学们对新冠肺炎知识的了解程度,决定随机抽取部分同学进行次问卷调查,并根据收集到的信息进行了统计,绘制了下面两.幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的同学共有 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)为了让全校师生都能更好地预防新冠肺炎,学生会准备组织一次宣讲活动,由问卷调查中“了解”的几名同学组成一个宣讲团,已知这几名同学中只有两个女生,若要在该宣讲团中任选两名同学在全校师生大会上作代表发言,请用列表或画树状图的方法,求选取的两名同学都是女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com