
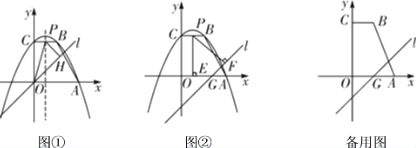
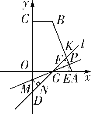
����Ŀ����2018֣��ģ�⣩��ͼ��������![]() ����
����![]() ����y�ύ�ڵ�C��
����y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2����ͼ�٣�ֱ��l�Ľ���ʽΪ![]() �������ߵĶԳ������߶�BC���ڵ�P������P��ֱ��l�Ĵ��ߣ�����Ϊ��H������OP����
�������ߵĶԳ������߶�BC���ڵ�P������P��ֱ��l�Ĵ��ߣ�����Ϊ��H������OP����![]() �������
�������
��3����ͼ���е�ֱ��![]() ����ƽ��4����λ���ȵõ�ֱ��
����ƽ��4����λ���ȵõ�ֱ��![]() ����ͼ�ڣ�ֱ��
����ͼ�ڣ�ֱ��![]() ��x�ύ�ڵ�G����P���ı���ABCO���ϵ�һ�㣬����P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F���Ƿ���ڵ�P��ʹ����P��E��FΪ������������ǵ��������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��x�ύ�ڵ�G����P���ı���ABCO���ϵ�һ�㣬����P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F���Ƿ���ڵ�P��ʹ����P��E��FΪ������������ǵ��������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ���
����3�����ڣ���![]() ����Ϊ(0��4)��
����Ϊ(0��4)��![]() ��(4��6)��
��(4��6)��![]() ��
��
��������
�⣺(1)��������![]() ����
����![]() ��
��
![]() ��
��
���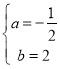 ��
��
�������ߵĽ���ʽΪ![]() ��
��
(2)�߸������ߵĶԳ���Ϊֱ��
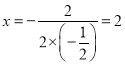 ��
��
![]() ��
��
���ͼ�٣��ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�
![]() ��
��
![]() ��
��
�ɵ�![]() ��
��
![]() ��
��
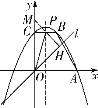
(3)�������������ĵ�![]() ����
����![]() ����Ϊ(0��4)��
����Ϊ(0��4)��![]() ��(4��6)��
��(4��6)��![]() ʱ����
ʱ����![]() Ϊ������������ǵ��������Σ�
Ϊ������������ǵ��������Σ�
[�ⷨ��ʾ]��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ����
����![]() ��
��
����������������ĵ�![]() ��
��
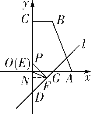
(a)����![]() ���߶�
���߶�![]() ��ʱ�����ͼ����ʾ����ʱ��
��ʱ�����ͼ����ʾ����ʱ��![]() ���
���![]() �غϣ�
�غϣ�
��![]() ��
��
��![]() ��
��
![]() ��
��
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() ��
��
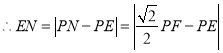 ��
��
��![]() ��
�У�
![]()
![]() ��
��
��![]() ����
����![]() �����
�����![]() ���ʴ������β����ڣ�
���ʴ������β����ڣ�
��![]() ����
����
![]() ��
��
������![]() ��
��
��![]() �����������ʴ������β����ڣ�
�����������ʴ������β����ڣ�
��![]() ����
����
![]() ��
��
������![]() ����
����![]() �����
�����![]() ��
��
![]() ��
��
(b)����![]() ��
��![]() ����ʱ�����ͼ�ۣ���ʱ
����ʱ�����ͼ�ۣ���ʱ![]() ��
��
��![]() ��
��
����![]() �ֱ���
�ֱ���![]() �ڵ�
�ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��֪![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
![]() ��
��
![]() ��
��
�ཫ![]() ����
����![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
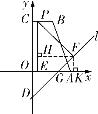
(c)����![]() ���߶�
���߶�![]() ��ʱ�����ͼ�ܣ�
��ʱ�����ͼ�ܣ�
![]() ��
��
������ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ
![]() ��
��
����![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
��(a)ͬ���������
![]() ��
��
��![]() ����
����![]() �����
�����![]() ���ʴ������β����ڣ�
���ʴ������β����ڣ�
��![]() ����
����
![]() ��
��
������![]() ����
����![]() �����
�����![]() ��������������ʱ
��������������ʱ![]() ��
��
��![]() ��
��
��![]() ��
��
������![]() ����
����![]() �����
�����![]() ���ʴ������β����ڣ�
���ʴ������β����ڣ�
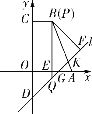
(d)����![]() ���߶�
���߶�![]() ��ʱ�����ͼ����ʾ��
��ʱ�����ͼ����ʾ��
![]() �ļн�Ϊ135����
�ļн�Ϊ135����
��ֻ������![]() ������
������
���![]() ��
��![]() ��ƽ�����ϣ�
��ƽ�����ϣ�
��˽�ƽ������![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ��
��![]() ֱ��
ֱ��![]() �ڵ�
�ڵ�![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
���![]() ��
��
![]() ��
��
��![]() ��
��
��ֱ��![]() �Ľ���ʽΪ��
�Ľ���ʽΪ��
![]() ��
��
����ֱ��![]() ��ֱ��
��ֱ��![]() ��
��
���![]() ��
��
(e)����![]() ��
��![]() ����ʱ����ʱ
����ʱ����ʱ![]() �����������β����ڣ�
�����������β����ڣ�
�����������������������ĵ�P���ҵ�![]() ����Ϊ��
������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
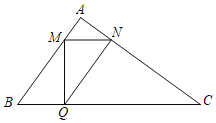
����Ŀ����ͼ����ABC�У���A��90����AB��3��AC��4����M��Q�ֱ��DZ�AB��BC�ϵĶ��㣨��M����A��B�غϣ�����MQ��BC������M��MN��BC����AC�ڵ�N������NQ����BQ��x��
��1���Ƿ����һ��Q��ʹ���ı���BMNQΪƽ���ı��Σ���˵�����ɣ�
��2����BM��2ʱ����x��ֵ��
��3����xΪ��ֵʱ���ı���BMNQ��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����
����![]() ����
Ϊ����![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() ��
��![]() �۵�����
�۵�����![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ��
��![]() �Ĵ��ߣ��ֱ�
�Ĵ��ߣ��ֱ�![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �����ȷֵ�ʱ��
�����ȷֵ�ʱ��![]() �ij�Ϊ_____________
�ij�Ϊ_____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������
������![]() ����
����![]() �����߶�
�����߶�![]() �ĶԳƵ�Ϊ��
�ĶԳƵ�Ϊ��![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ��
��![]() ��
��![]() ��
��![]() ����֪
����֪![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��ֵ��Сʱ����
��ֵ��Сʱ����![]() ��ֵΪ�� ��
��ֵΪ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
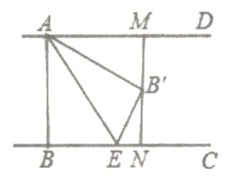
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() ���
���![]() ��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ΪԲ�ģ��߶�
ΪԲ�ģ��߶�![]() �ij�Ϊ�뾶��Բ�Ľ�Ϊ
�ij�Ϊ�뾶��Բ�Ľ�Ϊ![]() ������
������![]() ����
����![]() ������
������![]() ����ͼ����Ӱ���ֵ����Ϊ_______ƽ����λ��
����ͼ����Ӱ���ֵ����Ϊ_______ƽ����λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ֱ���y���x���ϣ�BC��AB����C�͵�O��ֱ��AB�����ࣩ����C������Ϊ(4��n)����C�ķ���������y=![]() ��x��0����ͼ��AC�ڵ�D(n+
��x��0����ͼ��AC�ڵ�D(n+![]() ��3)��
��3)��

��1�����������ı���ʽ��
��2�����B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
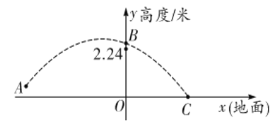
����Ŀ��2019��Ů�����籭��9�����ձ����У��й�Ů����ʮһ��ʤ�Ľ��˳ɼ�����ھ������չ�����Ŷ�Э������ǿƴ����Ů�ž�����ͼ��ij�α����е���ʱ�Ķ��������������������˶�·�߽��ƵĿ��������ߣ���ͬһ��ֱƽ���ڽ�����ͼ��ʾ��ֱ������ϵ����֪�˶�Ա����ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�
����������ˮƽ����Ϊ5�ף����������Ĵ�ֱ����Ϊ0.5�ף������������϶�0.26�״���ͼ�е�![]() ��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�
��Խ��������Ů���������������϶˾����ĸ߶�Ϊ2.24�ף������ʱ��ͼ�е�![]() ����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��
����������ˮƽ����Ϊ2.5�ף��������˶�·�ߵĺ�������ʽΪ�� ��

A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ�����ȫ����������������ʡ�����������������У�������ˮ�����������ȹ���A��B������ˮ�����豸��20̨���Գ����ܱ���ˮ���д�������֪ÿ̨A���豸�۸�Ϊ12��Ԫ��ÿ̨B���豸�۸�Ϊ10��Ԫ��1̨A���豸��2̨B���豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A���豸��3̨B���豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2��Ҫ��ʹ��ˮ�����������豸���ʽ���230��Ԫ����ÿ�ܴ�����ˮ�����ֲ�����4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������������˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com