
ЁОЬтФПЁПдкДДНЈЁАШЋЙњЮФУїГЧЪаЁБКЭЁАЪЁМЖЮФУїГЧЧјЁБЙ§ГЬжаЃЌГЧЧјЮлЫЎДІРэГЇОіЖЈЯШЙКТђAЁЂBСНаЭЮлЫЎДІРэЩшБИЙВ20ЬЈЃЌЖдГЧЧјжмБпЮлЫЎНјааДІРэЃЎвбжЊУПЬЈAаЭЩшБИМлИёЮЊ12ЭђдЊЃЌУПЬЈBаЭЩшБИМлИёЮЊ10ЭђдЊЃЛ1ЬЈAаЭЩшБИКЭ2ЬЈBаЭЩшБИУПжмПЩвдДІРэЮлЫЎ640ЖжЃЌ2ЬЈAаЭЩшБИКЭ3ЬЈBаЭЩшБИУПжмПЩвдДІРэЮлЫЎ1080ЖжЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНаЭЮлЫЎДІРэЩшБИУПжмЗжБ№ПЩвдДІРэЮлЫЎЖрЩйЖжЃП
ЃЈ2ЃЉвЊЯыЪЙЮлЫЎДІРэГЇЙКТђЩшБИЕФзЪН№ВЛГЌЙ§230ЭђдЊЃЌЕЋУПжмДІРэЮлЫЎЕФСПгжВЛЕЭгк4500ЖжЃЌЧыФуСаОйГіЫљгаЙКТђЗНАИЃЌВЂжИГіФФжжЗНАИЫљашзЪН№зюЩйЃПзюЩйЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉAЁЂBСНаЭЮлЫЎДІРэЩшБИУПжмЗжБ№ПЩвдДІРэЮлЫЎ240ЖжЁЂ200ЖжЃЛЃЈ2ЃЉЫљгаЙКТђЗНАИМћНтЮіЃЌЙКТђAаЭЮлЫЎДІРэЩшБИ13ЬЈЃЌBаЭЮлЫЎДІРэЩшБИ7ЬЈЪБЃЌЫљашЙКТђзЪН№зюЩйЃЌзюЩйЪЧ226ЭђдЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉБОЬтгаСНИіЯрЕШЙиЯЕЃК1ЬЈAаЭЩшБИУПжмДІРэЕФЮлЫЎ+2ЬЈBаЭЩшБИУПжмДІРэЕФЮлЫЎ=640ЖжЃЌ2ЬЈAаЭЩшБИУПжмДІРэЕФЮлЫЎ+3ЬЈBаЭЩшБИУПжмДІРэЕФЮлЫЎ=1080ЖжЃЌОнДЫЩшЮДжЊЪ§СаЗНГЬзщНтД№МДПЩЃЛ
ЃЈ2ЃЉЩшЙКТђAаЭЮлЫЎДІРэЩшБИxЬЈЃЌИљОнЙКТђЩшБИЕФзЪН№ВЛГЌЙ§230ЭђдЊЃЌЕЋУПжмДІРэЮлЫЎЕФСПгжВЛЕЭгк4500ЖжМДПЩСаГіЙигкxЕФВЛЕШЪНзщЃЌНтВЛЕШЪНзщЧѓГіxЕФЗЖЮЇКѓЃЌдйНсКЯxЮЊећЪ§МДПЩЧѓГіЫљгаЙКТђЗНАИЃЌНјвЛВНМДПЩЧѓГіНсЙћЃЎ
НтЃКЃЈ1ЃЉЩшAаЭЮлЫЎДІРэЩшБИУПжмУПЬЈПЩвдДІРэЮлЫЎxЖжЃЌBаЭЮлЫЎДІРэЩшБИУПжмУПЬЈПЩвдДІРэЮлЫЎyЖжЃЌИљОнЬтвтЃЌ
ЕУ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКAаЭЮлЫЎДІРэЩшБИУПжмУПЬЈПЩвдДІРэЮлЫЎ240ЖжЃЌBаЭЮлЫЎДІРэЩшБИУПжмУПЬЈПЩвдДІРэЮлЫЎ200ЖжЃЛ
ЃЈ2ЃЉЩшЙКТђAаЭЮлЫЎДІРэЩшБИxЬЈЃЌдђЙКТђBаЭЮлЫЎДІРэЩшБИЃЈ20ЉxЃЉЬЈЃЌ
дђ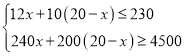 ЃЌ НтЕУЃК12.5ЁмxЁм15ЃЌ
ЃЌ НтЕУЃК12.5ЁмxЁм15ЃЌ
ЁпxЮЊећЪ§ЃЌЁрx=13ЃЌ14ЃЌ15ЃЌЙЪЙВгаШ§жжЙКТђЗНАИЃК
ЕквЛжжЗНАИЃКЕБx=13ЪБЃЌ20Љx=7ЃЌЛЈЗбЕФЗбгУЮЊЃК13ЁС12+7ЁС10=226ЭђдЊЃЛ
ЕкЖўжжЗНАИЃКЕБx=14ЪБЃЌ20Љx=6ЃЌЛЈЗбЕФЗбгУЮЊЃК14ЁС12+6ЁС10=228ЭђдЊЃЛ
ЕкШ§жжЗНАИЃКЕБx=15ЪБЃЌ20Љx=5ЃЌЛЈЗбЕФЗбгУЮЊЃК15ЁС12+5ЁС10=230ЭђдЊЃЛ
МДЙКТђAаЭЮлЫЎДІРэЩшБИ13ЬЈЃЌЙКТђBаЭЮлЫЎДІРэЩшБИ7ЬЈЪБЃЌЫљашЙКТђзЪН№зюЩйЃЌзюЩйЪЧ226ЭђдЊЃЎ


 ПЊаФЭмзДдЊзївЕЯЕСаД№АИ
ПЊаФЭмзДдЊзївЕЯЕСаД№АИ ПЮЪБеЦПиЫцЬУСЗЯАЯЕСаД№АИ
ПЮЪБеЦПиЫцЬУСЗЯАЯЕСаД№АИ вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ
вЛПЮвЛСЗвЛБОЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() ЃЌ
ЃЌ![]() ЃЌ
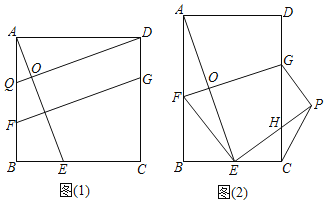
ЃЌ![]() ЃЎЕуPЪЧЦНУцФкВЛгыЕуAЃЌCжиКЯЕФШЮвтвЛЕуЃЎСЌНгAPЃЌНЋЯпЖЮAPШЦЕуPФцЪБеыа§зЊІСЕУЕНЯпЖЮDPЃЌСЌНгADЃЌBDЃЌCPЃЎ
ЃЎЕуPЪЧЦНУцФкВЛгыЕуAЃЌCжиКЯЕФШЮвтвЛЕуЃЎСЌНгAPЃЌНЋЯпЖЮAPШЦЕуPФцЪБеыа§зЊІСЕУЕНЯпЖЮDPЃЌСЌНгADЃЌBDЃЌCPЃЎ
ЃЈ1ЃЉЙлВьВТЯы
ШчЭМ1ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЪЧЁЁ ЁЁЃЌжБЯпBDгыжБЯпCPЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧЁЁ ЁЁЃЎ
ЕФжЕЪЧЁЁ ЁЁЃЌжБЯпBDгыжБЯпCPЯрНЛЫљГЩЕФНЯаЁНЧЕФЖШЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉРрБШЬНОП
ШчЭМ2ЃЌЕБ![]() ЪБЃЌЧыаДГі
ЪБЃЌЧыаДГі![]() ЕФжЕМАжБЯпBDгыжБЯпCPЯрНЛЫљГЩЕФаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ЕФжЕМАжБЯпBDгыжБЯпCPЯрНЛЫљГЩЕФаЁНЧЕФЖШЪ§ЃЌВЂОЭЭМ2ЕФЧщаЮЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
ЕБ![]() ЪБЃЌШєЕуEЃЌFЗжБ№ЪЧCAЃЌCBЕФжаЕуЃЌЕуPдкжБЯпEFЩЯЃЌЧыжБНгаДГіЕуCЃЌPЃЌDдкЭЌвЛжБЯпЩЯЪБ
ЪБЃЌШєЕуEЃЌFЗжБ№ЪЧCAЃЌCBЕФжаЕуЃЌЕуPдкжБЯпEFЩЯЃЌЧыжБНгаДГіЕуCЃЌPЃЌDдкЭЌвЛжБЯпЩЯЪБ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
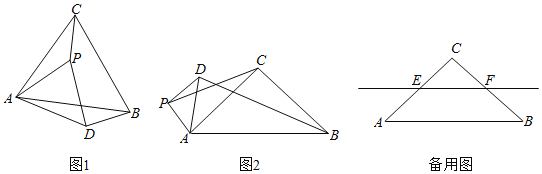
ЁОЬтФПЁПЃЈ2018жЃжнФЃФтЃЉШчЭМЃЌХзЮяЯп![]() Й§Еу
Й§Еу![]() ЃЌгыyжсНЛгкЕуCЃЎ
ЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ЃЌХзЮяЯпЕФЖдГЦжсгыЯпЖЮBCНЛгкЕуPЃЌЙ§ЕуPзїжБЯпlЕФДЙЯпЃЌДЙзуЮЊЕуHЃЌСЌНгOPЃЌЧѓ
ЃЌХзЮяЯпЕФЖдГЦжсгыЯпЖЮBCНЛгкЕуPЃЌЙ§ЕуPзїжБЯпlЕФДЙЯпЃЌДЙзуЮЊЕуHЃЌСЌНгOPЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉАбЭМЂйжаЕФжБЯп![]() ЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНжБЯп
ЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНжБЯп![]() ЃЌШчЭМЂкЃЌжБЯп
ЃЌШчЭМЂкЃЌжБЯп![]() гыxжсНЛгкЕуGЃЎЕуPЪЧЫФБпаЮABCOБпЩЯЕФвЛЕуЃЌЙ§ЕуPЗжБ№зїxжсЁЂжБЯпlЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуEЁЂFЃЎЪЧЗёДцдкЕуPЃЌЪЙЕУвдPЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
гыxжсНЛгкЕуGЃЎЕуPЪЧЫФБпаЮABCOБпЩЯЕФвЛЕуЃЌЙ§ЕуPЗжБ№зїxжсЁЂжБЯпlЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуEЁЂFЃЎЪЧЗёДцдкЕуPЃЌЪЙЕУвдPЁЂEЁЂFЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020ФъДКНкЧАЯІЁАаТаЭЙкзДВЁЖОЁББЌЗЂЃЎвпЧщОЭЪЧУќСюЃЌЗРПиОЭЪЧЪЙУќЃЌШЋЙњИїЕиГлдЎЮфККЕФвНЛЄЙЄзїепЃЌМљаавНепШЪаФЕФЪЙУќгыЕЃЕБЃЌЩсаЁМвЃЌЮЊДѓМвЃЌгУздМКЕФзЈвЕжЊЪЖгыбЊШтжЎЧћЙЙжўЦ№ШЋЩчЛсПЙЛївпЧщЕФИжЬњГЄГЧЃЎШчЭМСНЗљЭМЪЧ2дТ9ШеЕБЬьШЋЙњВПЗжЪЁЪаГлдЎЮфККвНЛЄЙЄзїепЕФШЫЪ§ЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
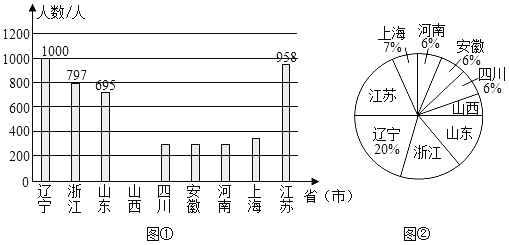
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЂйЩЯЪіЪЁЪа2дТ9ШеЕБЬьГлдЎЮфККЕФвНЛЄЙЄзїепЕФзмШЫЪ§ЮЊЁЁ ЁЁШЫЃЛ
ЂкЧыНЋЭМЂйЕФЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЧыЧѓГіЭМЂкЕФЩШаЮЭГМЦЭМжаЁАЩНЮїЁБЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉБОДЮКгББГлдЎЮфККЕФвНЛЄЙЄзїепжаЃЌга5ШЫБЈУћШЅжижЂЧјЃЌЭѕвНЩњКЭРювНЩњОЭдкЦфжаЃЌШєДгБЈУћЕФ5ШЫжаЫцЛњАВХХ2ШЫЃЌЧѓЭЌЪБАВХХЭѕвНЩњКЭРювНЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
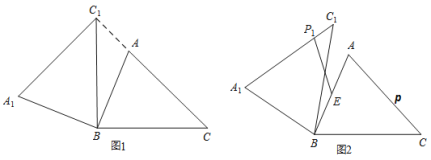
ЁОЬтФПЁПЃЈ1ЃЉжЄУїЭЦЖЯЃКШчЭМЃЈ1ЃЉЃЌдке§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЃЌ
ЃЌ![]() ЩЯЃЌ
ЩЯЃЌ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЃЌ
ЃЌ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЎ
ЃЎ
ЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЭЦЖЯЃК![]() ЕФжЕЮЊЁЁ ЁЁЃЛ
ЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉРрБШЬНОПЃКШчЭМЃЈ2ЃЉЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЉЃЎНЋОиаЮ
ЮЊГЃЪ§ЃЉЃЎНЋОиаЮ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпЩЯЕФЕу
БпЩЯЕФЕу![]() ДІЃЌЕУЕНЫФБпаЮ
ДІЃЌЕУЕНЫФБпаЮ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎЪдЬНОП
ЃЎЪдЬНОП![]() гы
гы![]() CPжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
CPжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙгІгУЃКдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌШє
ЪБЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШёНЧ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊЃЌЕУЕН
АДФцЪБеыЗНЯђа§зЊЃЌЕУЕН![]() ЃЎЃЈ1ЃЉШчЭМ1ЃЌЕБЕу
ЃЎЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФбгГЄЯпЩЯЪБЃЌдђ
ЕФбгГЄЯпЩЯЪБЃЌдђ![]() ЕФЖШЪ§ЮЊ______________ЖШЃЛЃЈ2ЃЉШчЭМ2ЃЌЕу
ЕФЖШЪ§ЮЊ______________ЖШЃЛЃЈ2ЃЉШчЭМ2ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() жаЕуЃЌЕу
жаЕуЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌдк
ЩЯЕФЖЏЕуЃЌдк![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊЙ§ГЬжаЃЌЕу
АДФцЪБеыЗНЯђа§зЊЙ§ГЬжаЃЌЕу![]() ЕФЖдгІЕуЪЧЕу
ЕФЖдгІЕуЪЧЕу![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ГЄЖШзюаЁжЕЪЧ_____________ЃЎ
ГЄЖШзюаЁжЕЪЧ_____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЕМфга20УћЙЄШЫЃЌФГЬьЫћУЧЩњВњЕФСуМўИіЪ§ЭГМЦШчЯТБэЃЎ
ГЕМф20УћЙЄШЫФГвЛЬьЩњВњЕФСуМўИіЪ§ЭГМЦБэ
ЩњВњСуМўЕФИіЪ§ЃЈИіЃЉ | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
ЙЄШЫШЫЪ§ЃЈШЫЃЉ | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
ЃЈ1ЃЉЧѓетвЛЬь20УћЙЄШЫЩњВњСуМўЕФЦНОљИіЪ§ЃЛ
ЃЈ2ЃЉЮЊСЫЬсИпДѓЖрЪ§ЙЄШЫЕФЛ§МЋадЃЌЙмРэепзМБИЪЕааЁАУПЬьЖЈЖюЩњВњЃЌГЌВњгаНБЁБЕФДыЪЉЃЎШчЙћФуЪЧЙмРэепЃЌДгЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЕФНЧЖШНјааЗжЮіЃЌФуНЋШчКЮШЗЖЈетИіЁАЖЈЖюЁБЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
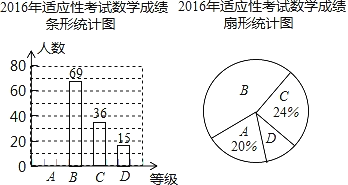
ЁОЬтФПЁПФГаЃЮЊСЫНтОХФъМЖбЇЩњ2020ФъЪЪгІадПМЪдЪ§бЇГЩМЈЃЌЯжДгОХФъМЖбЇЩњжаЫцЛњГщШЁВПЗжбЇЩњЕФЪЪгІадПМЪдЪ§бЇГЩМЈЃЌАДAЃЌBЃЌCЃЌDЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЭМЫљЪОВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭГМЦЭМжаЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉДЫДЮГщВщЕФбЇЩњШЫЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉАбЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєИУаЃОХФъМЖгабЇЩњ1200ШЫЃЎЧыЙРМЦдкетДЮЪЪгІадПМЪджаДяЕНBЕШМЖвдЩЯЃЈКЌBЕШМЖЃЉЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГдТЪГЦЗМгЙЄГЇвд2ЭђдЊв§НјвЛЬѕаТЕФЩњВњМгЙЄЯпЃЎвбжЊМгЙЄетжжЪГЦЗЕФГЩБОМлУПДќ20дЊЃЌЮяМлВПУХЙцЖЈЃКИУЪГЦЗЕФЪаГЁЯњЪлМлВЛЕУИпгкУПДќ35дЊЃЌШєИУЪГЦЗЕФдТЯњЪлСПyЃЈЧЇДќЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЮЊЃКyЃН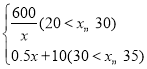 ЃЈдТЛёРћЃНдТЯњЪлЪеШыЉЩњВњГЩБОЉЭЖзЪГЩБОЃЉЃЎ
ЃЈдТЛёРћЃНдТЯњЪлЪеШыЉЩњВњГЩБОЉЭЖзЪГЩБОЃЉЃЎ
ЃЈ1ЃЉЕБЯњЪлЕЅМлЖЈЮЛ25дЊЪБЃЌИУЪГЦЗМгЙЄГЇЕФдТЯњСПЮЊЖрЩйЧЇДќЃЛ
ЃЈ2ЃЉЧѓИУМгЙЄГЇЕФдТЛёРћMЃЈЧЇдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЧѓЯњЪлЕЅМлЗЖЮЇдк30ЃМxЁм35ЪБЃЌИУМгЙЄГЇЪЧгЏРћЛЙЪЧПїЫ№ЃПШєгЏРћЃЌЧѓГізюДѓРћШѓЃЛШєПїЫ№ЃЌзюаЁПїЫ№ЪЧЖрЩйЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com