
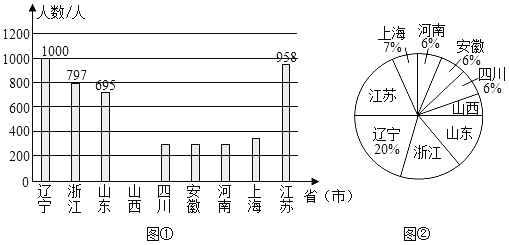
【题目】2020年春节前夕“新型冠状病毒”爆发.疫情就是命令,防控就是使命,全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.如图两幅图是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为 人;
②请将图①的条形统计图补充完整;
(2)请求出图②的扇形统计图中“山西”所对应扇形的圆心角的度数;
(3)本次河北驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
【答案】(1)①5000;②见解析;(2)21.6°;(3)![]()
【解析】
(1)①根据辽宁的人数和所占的百分比求出2月9日当天驰援武汉的医护工作者的总人数;
②先求出江苏、浙江和山东所占的百分比,再用整体1减去各省份所占的百分比,求出山西所占的百分比,再用总人数乘以山西所占的百分比即可补全统计图;
(2)用山西所占的百分比乘以360°即可得出答案;
(3)根据题意画出树状图得出所有等情况数和同时安排王医生和李医生的情况数,然后根据概率公式即可得出答案.
解:(1)①2月9日当天驰援武汉的医护工作者的总人数为![]() =5000(人),
=5000(人),
②江苏所占的百分比是:![]() ×100%=19.16%;
×100%=19.16%;
浙江所占的百分比是:![]() ×100%=15.94%;
×100%=15.94%;
山东所占的百分比是:![]() ×100%=13.9%;
×100%=13.9%;
则山西所占的百分比是:1﹣19.16%﹣7%﹣6%﹣6%﹣6%﹣13.9%﹣15.94%﹣20%=6%,
山西的人数是5000×6%=300(人),补图如下:
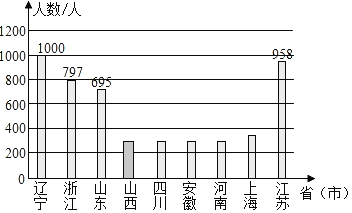
故答案为:5000;
(2)“山西”所对应扇形的圆心角的度数是360°×6%=21.6°;
(3)这5名医护工作者分别用1,2,3,4,5表示,其中王医生用1表示,李医生用2表示,根据题意画图如下:
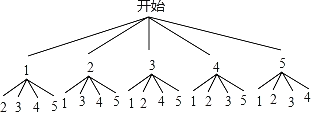
共有20种等情况数,其中同时安排王医生和李医生的有2种,
则同时安排王医生和李医生的概率是![]() =
=![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
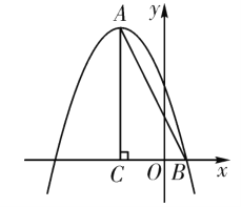
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,使
,使![]() .
.
①求点![]() 的坐标和
的坐标和![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,直接写出符合条件的所有点
为直角三角形?若存在,直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,点
,点![]() 关于线段
关于线段![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,连接
上的一个动点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 的值最小时,则
的值最小时,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在y轴和x轴上,BC⊥AB(点C和点O在直线AB的两侧),点C的坐标为(4,n)过点C的反比例函数y=![]() (x>0)的图象交边AC于点D(n+
(x>0)的图象交边AC于点D(n+![]() ,3).
,3).

(1)求反比例函数的表达式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
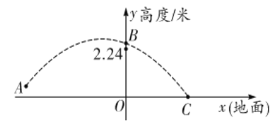
【题目】2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点![]() )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点
)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点![]() )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点
)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点![]() )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
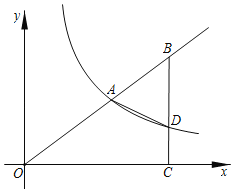
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与反比例函数的图象相交于点
与反比例函数的图象相交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求该反比例函数的解析式;
(2)若![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
⑴ 分别以点![]() (1,0),
(1,0),![]() (1,1),
(1,1),![]() (3,2)为圆心,1为半径作圆,得到⊙
(3,2)为圆心,1为半径作圆,得到⊙![]() ,⊙
,⊙![]() 和⊙
和⊙![]() ,其中是
,其中是![]() 的角内圆的是 ;
的角内圆的是 ;
⑵ 如果以点![]() (
(![]() ,2)为圆心,以1为半径的⊙
,2)为圆心,以1为半径的⊙![]() 为
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
⑶ 点![]() 在第一象限内,如果存在一个半径为1且过点
在第一象限内,如果存在一个半径为1且过点![]() (2,
(2,![]() )的圆为
)的圆为![]() 的角内相切圆,直接写出
的角内相切圆,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com