练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】车间有20名工人，某天他们生产的零件个数统计如下表．

    车间20名工人某一天生产的零件个数统计表

    生产零件的个数（个）

    9

    10

    11

    12

    13

    15

    16

    19

    20

    工人人数（人）

    1

    1

    6

    4

    2

    2

    2

    1

    1

    （1）求这一天20名工人生产零件的平均个数；

    （2）为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？

    【答案】（1）这一天20名工人生产零件的平均个数为13个；（2）定额为11个时，有利于提高大多数工人的积极性.

    【解析】

    （1）根据加权平均数的定义求解可得；

    （2）根据众数和中位数的定义求解，再分别从平均数、中位数和众数的角度，讨论达标人数和获奖人数情况，从而得出结论．

    解：（1）（个）

    答：这一天20名工人生产零件的平均个数为13个.

    （2）中位数为12个，众数为11个.

    当定额为13个时，有8个达标，6人获奖，不利于提高工人的积极性.

    当定额为12个时，有12个达标，8人获奖，不利于提高大多数工人的积极性.

    当定额为11个时，有18个达标，12人获奖，有利于提高大多数工人的积极性.

    ∴当定额为11个时，有利于提高大多数工人的积极性.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某县实施“村村通”工程中，决定在A、B两村之间修筑一条公路，甲、乙两个工程队分别从A、B两村同时开始修筑，施工期间，乙队因另有任务提前离开，余下的任务由甲队单独完成，直到道路修通，下图是甲、乙两个工程队修道路长度y（米）与修筑时间x（天）之间的函数图象，请根据图象所提供的信息，解答下列问题：

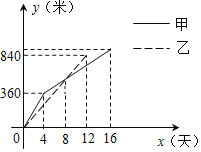
    （1）写出乙工程队修道路的长度y与修筑时间x之间的函数关系式：_____；

    （2）甲工程队前8天所修公路为_____米，该公路的总长度为_____米；

    （3）若乙工程队不提前离开，则两队只需_____天就能完成任务；

    （4）甲、乙两工程队第_____天时所修道路的长度相差80米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD =∠BCE = 90°，点M为AN的中点，过点E与AD平行的直线交射线AM于点N。

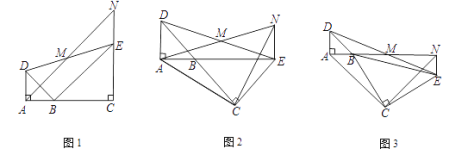
    （1）当A，B，C三点在同一直线上时（如图1），求证：AD=NE ；

    （2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；

    （3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，请证明；若不成立，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

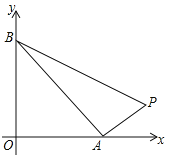
    【题目】如图，由点P（14,1），A（，0），B（0，）（），确定的△PAB的面积为18，则的值为_________，如果，则的值为_____________________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

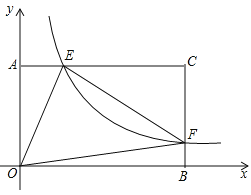
    【题目】在矩形AOBC中，OB=6，OA=4，分别以OB，OA所在直线为x轴和y轴建立如图所示的平面直角坐标系，F是BC上的一个动点（不与B、C重合），过F点的反比例函数（k＞0）的图象与AC边交于点E，连接OE，OF，EF．

    （1）若tan∠BOF=，求F点的坐标；

    （2）当点F在BC上移动时，△OEF与△ECF的面积差记为S，求当k为何值时，S有最大值，最大值是多少？

    （3）是否存在这样的点F，使得△OEF为直角三角形？若存在，求出此时点F坐标；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝kx＋6与x轴、y轴分别相交于点E，F，点E的坐标为(8，0)，点A的坐标为(6，0)，点P(x，y)是第一象限内直线上的一个动点(点P不与点E，F重合)．

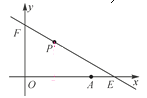
    (1)求k的值；

    (2)在点P运动的过程中，求出△OPA的面积S与x的函数关系式；

    (3)若△OPA的面积为，求此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次实验中，马达同学把一根弹簧的上端固定，在其下端悬挂物体质量的一组对应值.

    所挂物体质量

    0

    1

    2

    3

    4

    5

    弹簧长度

    18

    20

    22

    24

    26

    28

    （1）上表反应了哪两个变量之间的关系，并指出谁是自变量，谁是因变量.

    （2）当悬挂物体的重量为3千克时，弹簧长 ；不挂重物时弹簧长 .

    （3）弹簧长度所挂物体质量之间的关系可以用式子表示为： .

    （4）求挂物体时弹簧长度及弹簧长时所挂物体的重量.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C＝90°，CA＝CB， AG平分∠BAC交BC于H，BG⊥AG，垂足为G．若AH＝8，则BG的长为（ ）

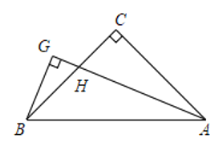
    A.3B.5C.8D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点O在△ABC内，且知OB和OC分别平分∠ABC和∠ACB，过O作直线EF分别交AB、AC于E、F．

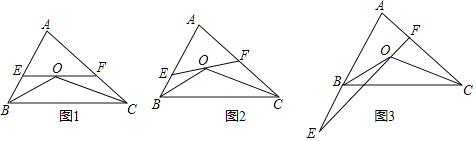
    （1）如图1，已知EF∥BC．

    ①若∠A＝76°，请直接写出∠BOE+∠COF的度数；

    ②猜想∠BOE、∠COF与∠A之间有怎样的数量关系？写出结论，不用证明

    （2）直线EF绕点O旋转到如图2的位置时（EF与BC不平行），那么上面（1）②中猜想的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由．

    （3）当直线EF绕点O旋转到如图3的位置时（点E在AB的延长线上），请直接写出∠BOE、∠COF与∠A之间的数量关系．

    查看答案和解析>>

    同步练习册答案