
【题目】如图,在△ABC中,∠C=90°,CA=CB, AG平分∠BAC交BC于H,BG⊥AG,垂足为G.若AH=8,则BG的长为( )
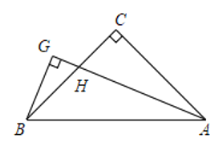
A.3B.5C.8D.4
【答案】D
【解析】
如图,延长AC交BG的延长线于E,构建等腰△BAE、全等三角形△BEC和△AHC,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=AH,所以BG=![]() AH=4.
AH=4.
如图,延长AC交BG的延长线于E,
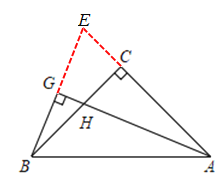
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠CAB=45°,
∵AG平分∠BAC
∴∠CAG=![]() ∠BAC=22.5°,
∠BAC=22.5°,
∵AG⊥BG,
∴∠BGA=90°,
∴∠GBA=90°-22.5°=67.5°,
∴∠GBC=∠EBA-∠ABC=22.5°.
∴∠GBC=∠CAH,
∵CA=CB,∠ACB=∠BCE
∴△ACH≌△BCE
∴BE=AH
∵AG平分∠BAC, AG⊥BG,
∴BG=EG,即BG=![]() BE,
BE,
∴BG=![]() AH=
AH=![]() ×8=4.
×8=4.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是( )

A. 2<AD<8B. 2<AD<4C. 1<AD<4D. 1<AD<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉二中广雅中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间m分成A、B、C、D四个等级(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
(1)C组的人数是 人,并补全条形统计图.
(2)本次调查的众数是 等,中位数落在 等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有 人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com