
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料:如图(1),在数轴上点![]() 示的数为
示的数为![]() 点表示的数为
点表示的数为![]() ,则点
,则点![]() 到点
到点![]() 的距离记为
的距离记为![]() ,线段
,线段![]() 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即![]()
![]()
解决问题:如图(2),数轴上点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,且有
,且有![]() ,点
,点![]() 表示的数是
表示的数是![]() .
.
![]()
(1)若数轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 表示的数为______.
表示的数为______.
(2)若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动到
个单位长度的速度向左运动到![]() ,同时点
,同时点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动分别到
个单位长度的速度向右运动分别到![]() ,假设
,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .则点
.则点![]() 表示的数是______,
表示的数是______,![]() =________
=________![]() 用含
用含![]() 的式子表示
的式子表示![]() .
.
(3)请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
(4)若点![]() 点
点![]() 分别以
分别以![]() 个单位每秒和
个单位每秒和![]() 个单位每秒的速度相向而行,则几秒后A、C两点相距
个单位每秒的速度相向而行,则几秒后A、C两点相距![]() 个单位长度?
个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
(2)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
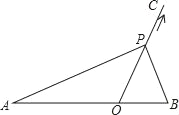
【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
A. ![]() B.
B. ![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]()
![]() 已知点
已知点![]() ,
,![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为
已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为![]() ,试求A,B两点间的距离;
,试求A,B两点间的距离;![]() 已知点
已知点![]() ,
,![]() ,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
,判断线段AB,BC,AC中哪两条是相等的?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
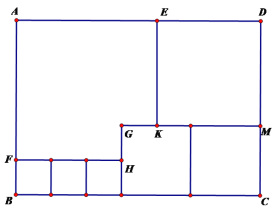
【题目】如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD,其中GH=1,GK=1,设BF=a.
(1)用含a的代数式表示CM=_____cm,DM=_______cm.
(2)用含a的代数式表示大长方形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月19日下午,安徽省政府在安徽省政务服务中心召开新闻发布会,发布2017年全省经济运行情况.2017年全省生产总值27518.7亿元,按可比价格计算,比上年增长8.5%.将27518.7亿元用科学记数法表示是( )
A. 2.75187×104 B. 2.75187×1011 C. 2.75187×1012 D. 2.75187×1013
查看答案和解析>>
科目:初中数学 来源: 题型:
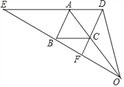
【题目】如图,已知DE∥BC,AO,DF交于点C.∠EAB=∠BCF.
(1)求证:AB∥DF;
(2)求证:OB2=OEOF;
(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com