
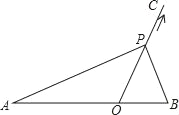
【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
A. ![]() B.
B. ![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
【答案】C
【解析】
根据题意分三种情况考虑:当∠A=90°;当∠B=90°;当∠APB=90°,根据△ABP为直角三角形,分别求出t的值即可.
解:分三种情况考虑:
当∠A=90°,即△ABP为直角三角形时,
∵∠BOC>∠A,且∠BOC=60°,
∴∠A≠90°,故此情况不存在;
当∠B=90°,即△ABP为直角三角形时,如图所示:
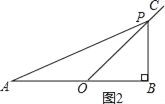
∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,
∵OP=2t,
∴t=1;
当∠APB=90°,即△ABP为直角三角形时,过P作PD⊥AB,
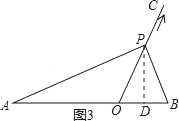
∴OD=OPcos∠BOC=t,PD=OPsin∠BOC=![]() t,
t,
∴AD=AO+OD=2+t,BD=OB﹣OD=1﹣t,即AB=3,
在Rt△ABP中,根据勾股定理得:
AP2+BP2=AB2,即(2+t)2+(![]() t)2+(
t)2+(![]() t)2+(1﹣t)2=32,
t)2+(1﹣t)2=32,
解得:t=![]() 或
或![]() (负值舍去),
(负值舍去),
综上,当t =1或t=![]() 时,△ABP是直角三角形.
时,△ABP是直角三角形.
故选:C.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
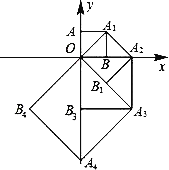
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA2A3B3,…,依此规律,则点A10的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段![]() (单位长度),线段
(单位长度),线段![]() (单位长度),点
(单位长度),点![]() 在数轴上表示的数是-10,点
在数轴上表示的数是-10,点![]() 在数轴上表示的数是16,若线段
在数轴上表示的数是16,若线段![]() 以每秒1个单位长度的速度向右匀速运动,同时线段
以每秒1个单位长度的速度向右匀速运动,同时线段![]() 以每秒3个单位长度的速度向左匀速运动,设运动时间为
以每秒3个单位长度的速度向左匀速运动,设运动时间为![]() 秒
秒
(1)当点![]() 与点
与点![]() 相遇时,点
相遇时,点![]() 、点
、点![]() 在数轴上表示的数分别为 ;
在数轴上表示的数分别为 ;
(2)当![]() 为何值时,点
为何值时,点![]() 刚好是
刚好是![]() 的中点
的中点

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
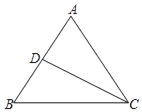
【题目】如图,在△ABC中,AB=AC,BC=8,tanB=![]() ,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
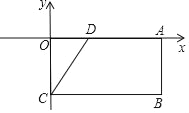
【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
(1)求过点B、C、D的抛物线的解析式;
(2)求出(1)中抛物线与x轴的另一个交点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“对称点”,如(2,﹣3)与(﹣3,2)是一对“对称点”.
(1)点(m,n)和它的“对称点“均在直线y=kx+a上,求k的值;
(2)直线y=kx+3与抛物线y=x2+bx+c的两个交点A,B恰好是“对称点”,其中点A在反比例函数y=![]() 的图象上,求此抛物线的解析式.
的图象上,求此抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com