Question

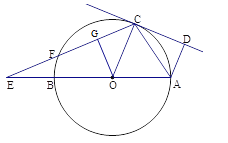
【题目】如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D.E是AB延长线上一点，CE交⊙O于点F，连结OC，AC.

(1)求证：AC平分∠DAO；

(2)若∠DAO=105°，∠E=30°.①求∠OCE的度数.②若⊙O的半径为，求线段EF的长.

Answer 1

【答案】（1）证明见解析；（2）①∠OCE=45°；②EF =-2.

【解析】【试题分析】（1）根据直线与⊙O相切的性质，得OC⊥CD.

又因为AD⊥CD，根据同一平面内，垂直于同一条直线的两条直线也平行，得：AD//OC. ∠DAC=∠OCA.又因为OC=OA，根据等边对等角，得∠OAC=∠OCA.等量代换得：∠DAC=∠OAC.根据角平分线的定义得：AC平分∠DAO.

（2）①因为 AD//OC，∠DAO=105°，根据两直线平行，同位角相等得，∠EOC=∠DAO=105°，在 中，∠E=30°，利用内角和定理，得：∠OCE=45°.

②作OG⊥CE于点G，根据垂径定理可得FG=CG， 因为OC=，∠OCE=45°.等腰直角三角形的斜边是腰长的 倍，得CG=OG=2. FG=2.在Rt△OGE中，∠E=30°，得GE=， 则EF=GE-FG=-2.

【试题解析】

（1）∵直线与⊙O相切，∴OC⊥CD.

又∵AD⊥CD，∴AD//OC.

∴∠DAC=∠OCA.

又∵OC=OA，∴∠OAC=∠OCA.

∴∠DAC=∠OAC.

∴AC平分∠DAO.

（2）解：①∵AD//OC，∠DAO=105°，∴∠EOC=∠DAO=105°

∵∠E=30°，∴∠OCE=45°.

②作OG⊥CE于点G，可得FG=CG

∵OC=，∠OCE=45°.∴CG=OG=2.

∴FG=2.

∵在Rt△OGE中，∠E=30°，∴GE=.

∴EF=GE-FG=-2.