
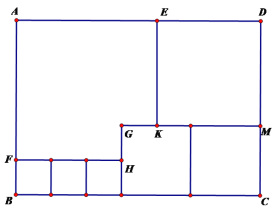
【题目】如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成大长方形ABCD,其中GH=1,GK=1,设BF=a.
(1)用含a的代数式表示CM=_____cm,DM=_______cm.
(2)用含a的代数式表示大长方形ABCD的周长.
【答案】(1)a+1;2a+1;(2)周长=16a+8.
【解析】
(1)根据图中可知CM=BF+GH,DM=KM=CM+(CM-GK)即可得出答案;
(2)结合(1)分别用含a的代数式表示出BC和CD即可求出答案.
解:(1)由图中可知CM=BF+GH,因为BF=a,GH=1,所以CM=a+1,
由图中可知DM=KM=CM+(CM-GK),因为CM=a+1,GK=1,所以CM-GK=a,所以DM=a+1+a=2a+1;
(2)由(1)可知DM=2a+1,CM=a+1,CD=DM+CM,
所以CD=3a+2,
由图中可知BC=3BF+2CM,所以BC=3a+2(a+1)=5a+2
所以长方形ABCD的周长为2(BC+CD)=2(3a+2+5a+2)=16a+8,
故答案为a+1;2a+1;周长=16a+8.


科目:初中数学 来源: 题型:
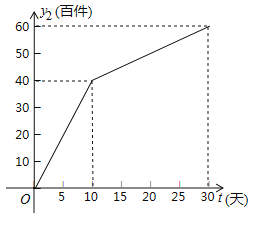
【题目】(2017湖北省荆门市)我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
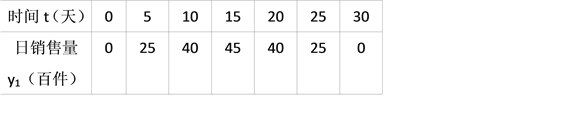
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为 ______________.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/4/1916730188324864/1920418179735552/STEM/955c40623e644964ae11bcb49c75f843.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
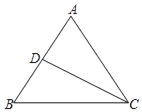
【题目】如图,在△ABC中,AB=AC,BC=8,tanB=![]() ,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
,点D是AB的中点,如果把△BCD沿直线CD翻折,使得点B落在同一平面内的B′处,联结A B′,那么A B′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 从
从![]() 出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点
出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点![]() 第
第![]() 次碰到矩形的边时,点
次碰到矩形的边时,点![]() 的坐标为( )
的坐标为( )

A. (0,3) B. (5,0) C. (1,4) D. (8,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
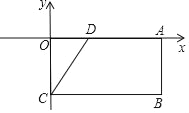
【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
(1)求过点B、C、D的抛物线的解析式;
(2)求出(1)中抛物线与x轴的另一个交点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
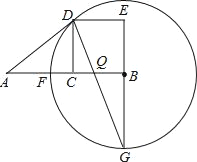
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com