
����Ŀ����֪��O����ABC�ڣ���֪OB��OC�ֱ�ƽ�֡�ABC�͡�ACB����O��ֱ��EF�ֱ�AB��AC��E��F��
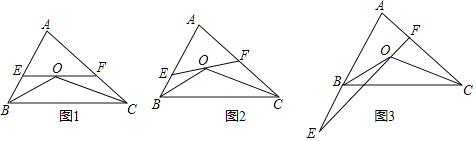
��1����ͼ1����֪EF��BC��
������A��76������ֱ��д����BOE+��COF�Ķ�����
�ڲ����BOE����COF���A֮����������������ϵ��д�����ۣ�����֤��
��2��ֱ��EF�Ƶ�O��ת����ͼ2��λ��ʱ��EF��BC��ƽ�У�����ô���棨1�����в���Ľ��ۻ���������������������֤�����������������˵�����ɣ�
��3����ֱ��EF�Ƶ�O��ת����ͼ3��λ��ʱ����E��AB���ӳ����ϣ�����ֱ��д����BOE����COF���A֮���������ϵ��
���𰸡���1����52�����ڡ�BOE+��COF��90����![]() ��A�����ɼ���������2�����������ɼ���������3����COF����BOE��90����
��A�����ɼ���������2�����������ɼ���������3����COF����BOE��90����![]() ��A
��A
��������
��1���ٸ���ƽ���ߵ����ʺ��������ڽǺͶ������м��㣻
���â��еķ��������Ƶ���ͬ������ƽ���ߵ����ʺ��������ڽǺͶ����ó��ǵĹ�ϵ��
��2�������������ڽǺͶ����Լ�ƽ�ǵ����ʼ���֤�á�BOE+��COF=90��-![]() ��A��
��A��
��3�������������ڽǺͶ����Լ�ƽ�ǵĶ��弴��֤�á�COF-��BOE=90��-![]() ��A.
��A.
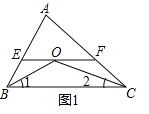
��1������ͼ1����EF��BC��
���BOE����1����COF����2��
��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB
��ACB
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A��
��A��
���BOE+��COF����1+��2��90����![]() ��A��90����
��A��90����![]() ��52����
��52����
�ڲ����BOE+��COF��90����![]() ��A��
��A��
֤������EF��BC��
���BOE����1����COF����2��
��OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB
��ACB
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A��
��A��
���BOE+��COF����1+��2��90����![]() ��A��
��A��
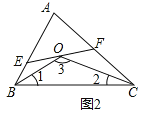
��2��������
֤������ͼ2����OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���1��![]() ��ABC����2��
��ABC����2��![]() ��ACB��
��ACB��
���1+��2��![]() ��ABC+
��ABC+![]() ��ACB��
��ACB��![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90����
��180������A����90����![]() ��A
��A
�ߡ�BOE+��COF+��3����1+��2+��3��180��
���BOE+��COF����1+��2��90����![]() ��A��
��A��
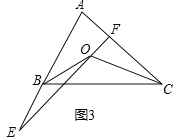
��3���⣺��ͼ3����OB��OC�ֱ�ƽ�֡�ABC�͡�ACB��
���OBC��![]() ��ABC����OCB��
��ABC����OCB��![]() ��ACB��
��ACB��
���BOC��180����![]() ��ABC+
��ABC+![]() ��ACB��180����
��ACB��180����![]() ����ABC+��ACB����
����ABC+��ACB����![]() ��180������A����90��+
��180������A����90��+![]() ��A��
��A��
�ߡ�BOC����BOE+��COF��180����
���COF����BOE��180������BOC��180������90��+![]() ��A����90����
��A����90����![]() ��A��
��A��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������20�����ˣ�ij�������������������ͳ�����±���
����20������ijһ���������������ͳ�Ʊ�
��������ĸ��������� | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
�����������ˣ� | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ��������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��

��1����֤����ABM�ס�EFA��
��2����AB=12��BM=5����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г�;����վÿ��6��30��7��30����ij�ص������Ʊ����ͬ�����������ʳ̶Ȳ�ͬ.С�ź�С������������һʱ�γ˳�ȥ���أ�����֪��������������˳�����˲��ò�ͬ�ij˳�������С��������ξ������������ĵ�һ��������С�������ȹ۲���ϳ�������һ��������ʱ�������ϳ���������ϸ�۲쳵������״��.���ڶ�������״���ȵ�һ�����ã������ϵڶ����������ڶ����������һ�����������ϵ�������.�����������������ʳ̶ȷ�Ϊ�š��С������ȣ�����˼�����ش��������⣺
(1)�����������ֵ��Ⱥ�˳�����ļ��ֿ��ܣ�
(2)���б��������ַ��������ŵȳ��Ŀ����Դ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��CAD����CEB���ǵȱ������Σ�BD��EA���ӳ����ཻ�ڵ�F��
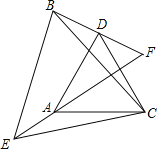
��1����֤����ACE�ա�DCB��
��2�����F�Ķ�����
��3����AD��BD����ֱ��д���߶�EF���߶�BD��DF֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�E��F��AD���ϵ��������㣬��AE=FD������BE��CF��BD��CF��BD���ڵ�H������DH�����н�����ȷ���ǣ�������
�١�ABG�ס�FDG ��HDƽ�֡�EHG ��AG��BE ��S��HDG��S��HBG=tan��DAG ���߶�DH����Сֵ��2![]() ��2
��2

A. �٢ڢ� B. �٢ۢܢ� C. �٢ڢܢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף�����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա��������գ����·ֱ���A��B��C��D��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в���������
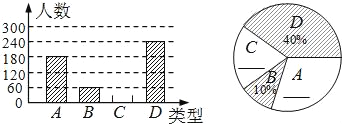
�����������Ϣ�ش�
��1�����βμӳ�������ľ����ж����ˣ�
��2����������������ͼ����������
��3��������ͳ��ͼ��C����Բ�ĽǵĶ�����
��4������������ȫ��ͬ��A��B��C��D�ո�һ���������С���������������б�����״ͼ�ķ����������ڶ����Ե���ǡ����C�յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���人���й�����ѧΪ���˽�ȫУѧ���Ŀ����Ķ�������������ȡ�˲���ѧ�������Ķ�ʱ����飬�ֽ�ѧ��ÿѧ�ڵ��Ķ�ʱ��m�ֳ�A��B��C��D�ĸ��ȼ���A�ȣ�90��m��100��B�ȣ�80��m��90��C�ȣ�60��m��80��D�ȣ�m��60����λ��Сʱ���������Ƴ�����ͼ��������������ͳ��ͼ������������Ϣ���ش��������⣺
��1��C����������� ���ˣ�����ȫ����ͳ��ͼ��
��2�����ε������������ ���ȣ���λ�������� ���ȣ�
��3�����ҹ涨������Сѧÿѧ�ڵĿ����Ķ�ʱ�䲻����60Сʱ���������У������3500��ѧ�����ﵽ���ҹ涨���Ķ�ʱ�������Լ���� ���ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��
��1��������ABC����y��ĶԳ�ͼ����A1B1C1��
��2���������ABC�������
��3��ֱ��д����ABC����x��ԳƵ���������A2B2C2�ĸ������꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com