
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点H,连接DH,下列结论正确的是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2![]() ﹣2
﹣2

A. ①②⑤ B. ①③④⑤ C. ①②④⑤ D. ①②③④
【答案】B
【解析】
首先证明△ABE≌△DCF,△ADG≌△CDG(SAS),△AGB≌△CGB,利用全等三角形的性质,等高模型、三边关系一一判断即可.
∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°.
∵在△ABE和△DCF中,AB=CD,∠BAD=∠ADC,AE=DF,
∴△ABE≌△DCF,
∴∠ABE=∠DCF.
∵在△ADG和△CDG中,AD=CD,∠ADB=∠CDB,DG=DG,
∴△ADG≌△CDG,
∴∠DAG=∠DCF,
∴∠ABE=∠DAG.
∵∠DAG+∠BAH=90°,
∴∠BAE+∠BAH=90°,
∴∠AHB=90°,
∴AG⊥BE,故③正确,
同理可证:△AGB≌△CGB.
∵DF∥CB,
∴△CBG∽△FDG,
∴△ABG∽△FDG,故①正确.
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD,∠DAG=∠FCD,
∴S△HDG:S△HBG=tan∠FCD=tan∠DAG,故④正确.
取AB的中点O,连接OD、OH.
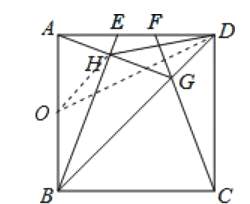
∵正方形的边长为4,
∴AO=OH=![]() ×4=2,
×4=2,
由勾股定理得,OD=![]() ,
,
由三角形的三边关系得,O、D、H三点共线时,DH最小,
DH最小=2![]() -2.
-2.
无法证明DH平分∠EHG,故②错误,
故①③④⑤正确.
故选B.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6与x轴、y轴分别相交于点E,F,点E的坐标为(8,0),点A的坐标为(6,0),点P(x,y)是第一象限内直线上的一个动点(点P不与点E,F重合).
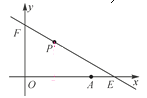
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式;
(3)若△OPA的面积为![]() ,求此时点P的坐标.
,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形纸片ABCD中,AB=3,BC=5.折叠纸片使点A落在边BC上的A′处,折痕为PQ.当点A′在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点A′在边BC上可移动的最大距离为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:在路上,我们经常看到这样的汽车牌照号:“辽A30803”,“辽P12321”,“京C76H67”,…,给人以对称美的感受.除了表示地区标志的汉字和字母(如:沈阳车牌辽A,葫芦岛车牌辽P等)以外,像“30803”、“76H67”这样的由数或由数和字母共同组成的车牌号,我们称之为“轴对称车牌号”.在正整数中,现定义为,“形如![]() 的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
(1)写出最小的五位“轴对称数”;
(2)请你设计一个我们葫芦岛市的车牌号,要求:此车牌号的后五位是“轴对称车牌号”,且由数字和字母组成的;
(3)已知某车的车牌号是由数字组成的“轴对称车牌号”,设首位数字为m,去掉首尾数字后的中间的三位数为n.已知多项式x2﹣2m能用公式法分解因式,![]() n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O在△ABC内,且知OB和OC分别平分∠ABC和∠ACB,过O作直线EF分别交AB、AC于E、F.
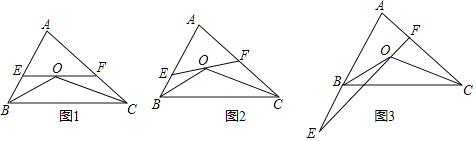
(1)如图1,已知EF∥BC.
①若∠A=76°,请直接写出∠BOE+∠COF的度数;
②猜想∠BOE、∠COF与∠A之间有怎样的数量关系?写出结论,不用证明
(2)直线EF绕点O旋转到如图2的位置时(EF与BC不平行),那么上面(1)②中猜想的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(3)当直线EF绕点O旋转到如图3的位置时(点E在AB的延长线上),请直接写出∠BOE、∠COF与∠A之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路列车(简称:高铁)是人们出行的重要交通工具:已知高铁平均速度是普通铁路列车(简称:普客)平均速度的的3倍.同样行驶690km,高铁比普客少用4.6h.
(1)求高铁的平均速度.
(2)某天王老师乘坐8:40出发的高铁,到里程1050km的A市参加当天14:00召开的会议.若他从A市高铁站到会议地点最多还需要1.5h,试问在高铁准点到达的情况下,他能在开会之前赶到会议地点吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD=![]() .
.
(1)求证:AE=CD;
(2)求sin∠CPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=
(k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=![]() ,点B的坐标(6,n).
,点B的坐标(6,n).
(1)求反比例函数和一次函数的解析式.
(2)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com