
【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
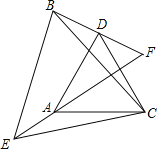
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
【答案】(1)见解析;(2)60°;(3)EF=BD+2DF.
【解析】
(1)根据等边三角形的性质得到CB=CE,CD=CA,∠BCE=∠DCA=60°,由全等三角形的判定定理即可得到结论;
(2)设BC与EF相交于G,根据全等三角形的性质得到∠1=∠2,根据三角形的内角和即可得到结论;
(3)根据垂直的定义得到∠ADF=90°,求得∠DAF=30°,根据直角三角形的性质得到AF=2DF,根据全等三角形的性质得到AE=BD,于是得到结论.
(1)∵△CAD与△CEB都是等边三角形,
∴CB=CE,CD=CA,∠BCE=∠DCA=60°,
∴∠BCD=∠ECA,
∴△ACE≌△DCB(SAS);
(2)设BC与EF相交于G,
由(1)可知△ACE≌△DCB,
∴∠1=∠2,
∵∠1+∠BGF+∠F=∠2+∠AGC+∠BCE=180°,
而∠BGF=∠AGC,
∴∠F=∠BCE=60°;
(3)EF=BD+2DF,理由如下:
∵AD⊥BD,
∴∠ADF=90°,
∵∠F=60°,
∴∠DAF=30°,
∴AF=2DF,
∵△ACE≌△DCB,
∴AE=BD,
∴EF=AE+AF=BD+2DF.


科目:初中数学 来源: 题型:
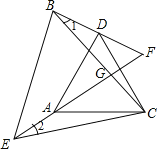
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是BC上的一个动点(不与B、C重合),过F点的反比例函数![]() (k>0)的图象与AC边交于点E,连接OE,OF,EF.
(k>0)的图象与AC边交于点E,连接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F点的坐标;
,求F点的坐标;
(2)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
(3)是否存在这样的点F,使得△OEF为直角三角形?若存在,求出此时点F坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若ACBC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m、n表示△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想我们曾经学习过的三角形外心的概念,我们可引入准外心的定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.请回答下面的三个问题:

(1)如图1,若PB=PC,则点P为△ABC的准外心,而且我们知道满足此条件的准外心有无数多个,你能否用尺规作出另外一个准外心Q呢?请尝试完成;
(2)如图2,已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长;
(3)如图3,点B既是△EDC又是△ADC的准外心,BD=BA=BC=2AD,BD∥AC,CD=![]() ,求AD的值.
,求AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买![]() 元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得
元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得![]() 元、
元、![]() 元、
元、![]() 元购物券,如果不愿转动转盘,那么可以直接获得
元购物券,如果不愿转动转盘,那么可以直接获得![]() 元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为
元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为![]() ,
,![]() ,
,![]() .
.
(1)平均来说,每转动转盘![]() 次所获得购物券的金额是多少?
次所获得购物券的金额是多少?
(2)小明在家也做了一个同样的试验,转动转盘![]() 次后共得购物前
次后共得购物前![]() 元,据此,小明认为,还是直接领取
元,据此,小明认为,还是直接领取![]() 元购物券合算,你同意他的说法吗?
元购物券合算,你同意他的说法吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O在△ABC内,且知OB和OC分别平分∠ABC和∠ACB,过O作直线EF分别交AB、AC于E、F.
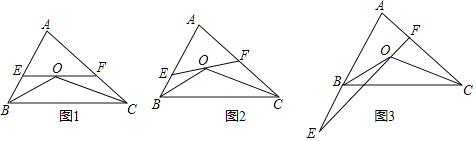
(1)如图1,已知EF∥BC.
①若∠A=76°,请直接写出∠BOE+∠COF的度数;
②猜想∠BOE、∠COF与∠A之间有怎样的数量关系?写出结论,不用证明
(2)直线EF绕点O旋转到如图2的位置时(EF与BC不平行),那么上面(1)②中猜想的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(3)当直线EF绕点O旋转到如图3的位置时(点E在AB的延长线上),请直接写出∠BOE、∠COF与∠A之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点.

(1)求这个二次函数以及直线BC的解析式;
(2)直接写出点A的坐标;
(3)当x为何值时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为![]() ,AC=2+2
,AC=2+2![]() ,则△CEF的面积为( )
,则△CEF的面积为( )

A. ![]() B. 2
B. 2![]() C. 2+
C. 2+![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的两个三角形,可以证明它们全等的是( ).
A.一边和这一边上的高对应相等B.两边和第三边上的中线对应相等
C.两边和其中一边的对角对应相等D.直角三角形的斜边对应相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com