
【题目】某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买![]() 元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得
元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得![]() 元、
元、![]() 元、
元、![]() 元购物券,如果不愿转动转盘,那么可以直接获得
元购物券,如果不愿转动转盘,那么可以直接获得![]() 元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为
元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为![]() ,
,![]() ,
,![]() .
.
(1)平均来说,每转动转盘![]() 次所获得购物券的金额是多少?
次所获得购物券的金额是多少?
(2)小明在家也做了一个同样的试验,转动转盘![]() 次后共得购物前
次后共得购物前![]() 元,据此,小明认为,还是直接领取
元,据此,小明认为,还是直接领取![]() 元购物券合算,你同意他的说法吗?
元购物券合算,你同意他的说法吗?
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
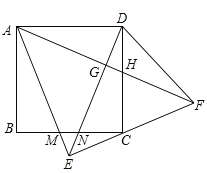
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于点G,交CD于点H,下列结论:①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤![]() ,其中正确的有__________.
,其中正确的有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么![]() 是方程N的一个根.
是方程N的一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
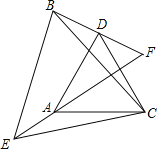
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
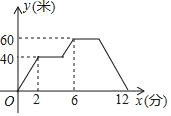
【题目】小明在练习操控航拍无人机,该型号无人机在上升和下落时的速度相同,设无人机的飞行高度为y(米),小明操控无人飞机的时间为x(分),y与x之间的函数图象如图所示.
(1)无人机上升的速度为 米/分,无人机在40米的高度上飞行了 分.
(2)求无人机下落过程中,y与x之间的函数关系式.
(3)求无人机距地面的高度为50米时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
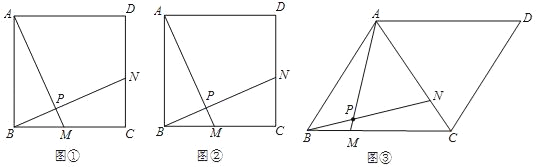
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里.

A. 15![]() +15 B. 30
+15 B. 30![]() +30 C. 45+15
+30 C. 45+15![]() D. 60
D. 60
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com