
【题目】如图,正方形ABCD中,以AD为底边作等腰△ADE,将△ADE沿DE折叠,点A落到点F处,连接EF刚好经过点C,再连接AF,分别交DE于点G,交CD于点H,下列结论:①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤![]() ,其中正确的有__________.
,其中正确的有__________.
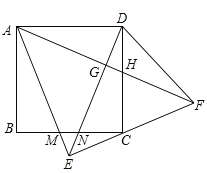
【答案】①③⑤
【解析】
①:由正方形ABCD的性质以及等腰△EAD的性质证明△ABM≌△DCN即可;②③:连接AC,以D为圆心,DA的长度为半径画圆,不难证明圆D过点A、E、F,由圆周角定理求出∠AFE的度数,进而求出∠FAE的度数及∠AEF的度数,从而证明出△AEF为等腰直角三角形,由折叠可得出∠AED的度数,由等腰△AED的性质求出∠DAE的度数即可求出∠DAF的度数;④:作CK⊥AF交AF于点K,不难求出∠KAC=∠CAE=22.5°,由角平分线的性质可得CK=CE,由直角三角形的性质可得CF>KC,所以CF>CE;⑤:求出∠FDC=∠ACD=45°,证明出DF∥AC,从而得出S△DAF=S△DCF,进而得出S△DAH=S△CFH.
∵正方形ABCD,
∴AB=CD,∠BAD=∠CDA=∠B=∠DCN=90°,
∵等腰△ADE,
∴∠EAD=∠EDA,
∴∠BAM=∠CDN,
∵在Rt△ABM与Rt△DCN中,
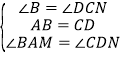 ,
,
∴△ABM≌△DCN,
故结论①正确;
连接AC,以D为圆心,DA的长度为半径画圆,
由翻折可得AD=DF,AE=EF,
∴圆D经过点A、C、F,
∴∠AFC=45°,
∴∠AFC=∠EAF=45°,
∴∠AEF=90°,
∴∠AED=∠DEF=45°,
∴∠EAD=67.5°,
∴∠DAF=22.5°,
故结论②错误;
∵AE=EF,∠AEF=90°,
∴△AEF是等腰直角三角形,
故结论③正确;
作CK⊥AF交AF于点K,
∵∠EAD=62.5°,∠FAD=22.5°,
∴∠BAM=∠CDN=22.5°,∠KAC=22.5°,
∴∠EAC=22.5°,
∴∠EAC=∠KAC,
∴KC=CE,
∵在Rt△FKC中,FC>KC,
∴FC>CE,
故结论④错误;
∵∠DAF=∠DFA=22.5°,
∴∠ADF=135°,
∴∠FDC=45°,
∴∠FDC=∠DCA,
∴AC∥DF,
∴S△DAF=S△DCF,
∴S△DAH=S△CFH,
故结论⑤正确.
正确的结论有①③⑤.

故答案为①③⑤.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
科目:初中数学 来源: 题型:
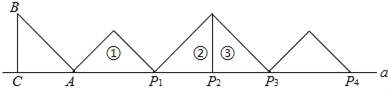
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+![]() …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
A. 1345+376![]() B. 2017+
B. 2017+![]() C. 2018+
C. 2018+![]() D. 1345+673
D. 1345+673![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为![]() 、
、![]() 、
、![]() ,若AD=2,AB=
,若AD=2,AB=![]() ,∠A=60°,则
,∠A=60°,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点C把线段AB分成两条线段AC和BC,如果![]() ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比。
,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比。
![]()
(2)已知:如图,已知△ABC∽△DEF,
求证:相似三角形面积的比等于相似比的平方

查看答案和解析>>
科目:初中数学 来源: 题型:
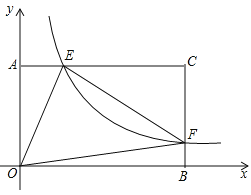
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是BC上的一个动点(不与B、C重合),过F点的反比例函数![]() (k>0)的图象与AC边交于点E,连接OE,OF,EF.
(k>0)的图象与AC边交于点E,连接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F点的坐标;
,求F点的坐标;
(2)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
(3)是否存在这样的点F,使得△OEF为直角三角形?若存在,求出此时点F坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:

(1)放入一个小球水面升高 ,![]() ,放入一个大球水面升高
,放入一个大球水面升高 ![]() ;
;
(2)如果要使水面上升到50![]() ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
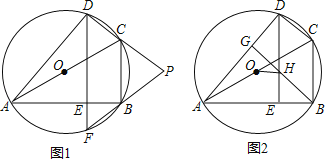
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买![]() 元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得
元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得![]() 元、
元、![]() 元、
元、![]() 元购物券,如果不愿转动转盘,那么可以直接获得
元购物券,如果不愿转动转盘,那么可以直接获得![]() 元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为
元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为![]() ,
,![]() ,
,![]() .
.
(1)平均来说,每转动转盘![]() 次所获得购物券的金额是多少?
次所获得购物券的金额是多少?
(2)小明在家也做了一个同样的试验,转动转盘![]() 次后共得购物前
次后共得购物前![]() 元,据此,小明认为,还是直接领取
元,据此,小明认为,还是直接领取![]() 元购物券合算,你同意他的说法吗?
元购物券合算,你同意他的说法吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com