
【题目】结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若ACBC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m、n表示△ABC的面积.

【答案】(1)证明见解析;(2)证明见解析;(3)S△ABC=![]() mn;
mn;
【解析】
(1)设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,仿照例题利用勾股定理得(x+m)2+(x+n)2=(m+n)2,再根据S△ABC=![]() AC×BC,即可证明S△ABC=mn.(2)由ACBC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)过点A作AG⊥BC于点G,在Rt△ACG中,根据条件求出AG、CG,又根据BG=BC-CG得到BG .在Rt△ABG中,根据勾股定理可得x2+(m+n)x=3mn,由此S△ABC=
AC×BC,即可证明S△ABC=mn.(2)由ACBC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)过点A作AG⊥BC于点G,在Rt△ACG中,根据条件求出AG、CG,又根据BG=BC-CG得到BG .在Rt△ABG中,根据勾股定理可得x2+(m+n)x=3mn,由此S△ABC=![]() BCAG=
BCAG=![]() mn.
mn.
设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,
根据切线长定理,得:AE=AD=m、BF=BD=n、CF=CE=x,
(1)如图1,
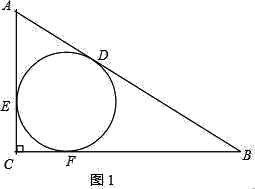
在Rt△ABC中,根据勾股定理,得:(x+m)2+(x+n)2=(m+n)2,
整理,得:x2+(m+n)x=mn,
所以S△ABC=![]() ACBC
ACBC
=![]() (x+m)(x+n)
(x+m)(x+n)
= ![]() [x2+(m+n)x+mn]
[x2+(m+n)x+mn]
=![]() (mn+mn)
(mn+mn)
=mn;
(2)由ACBC=2mn,得:(x+m)(x+n)=2mn,
整理,得:x2+(m+n)x=mn,
∴AC2+BC2=(x+m)2+(x+n)2
=2[x2+(m+n)x]+m2+n2
=2mn+m2+n2
=(m+n)2
=AB2,
根据勾股定理逆定理可得∠C=90°;
(3)如图2,过点A作AG⊥BC于点G,
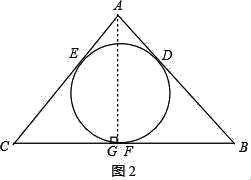
![]() (x+m),CG=ACcos60°=
(x+m),CG=ACcos60°=![]() (x+m),
(x+m),
∴BG=BC﹣CG=(x+n)﹣![]() (x+m),
(x+m),
在Rt△ABG中,根据勾股定理可得:[![]() (x+m)]2+[(x+n)﹣
(x+m)]2+[(x+n)﹣![]() (x+m)]2=(m+n)2,
(x+m)]2=(m+n)2,
整理,得:x2+(m+n)x=3mn,
∴S△ABC=![]() BCAG
BCAG
=![]() ×(x+n)
×(x+n)![]() (x+m)
(x+m)
=![]() [x2+(m+n)x+mn]
[x2+(m+n)x+mn]
=![]() ×(3mn+mn)
×(3mn+mn)
=![]() mn.
mn.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点![]() 的坐标为__________,图2中
的坐标为__________,图2中![]() 的值为__________.
的值为__________.


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么![]() 是方程N的一个根.
是方程N的一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
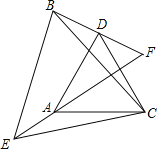
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com