
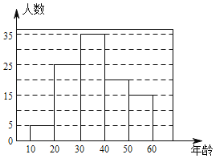
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
【答案】(1)25,20,126;(2)补全的频数分布直方图如图所示;见解析;(3)40~50岁年龄段的关注本次大会的人数约有60万人.
【解析】
(1)随机选取总人数减去其他组人数即可得到a,第4组人数除以调查总人数即可得到答案;第3组人数所占百分比乘以360度,即可得到答案;
(2)由(1)值,![]() 有25人,即可得到答案;
有25人,即可得到答案;
(3)300万乘以调查40~50岁年龄段的百分比可得答案.
(1)![]() ,
,
![]() ,
,
第3组人数在扇形统计图中所对应的圆心角是:![]() ,
,
故答案为:25,20,126;
(2)由(1)值,![]() 有25人,
有25人,
补全的频数分布直方图如图所示;
(3)![]() (万人),
(万人),
答:40~50岁年龄段的关注本次大会的人数约有60万人.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
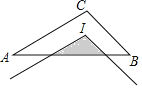
A. 4.5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级![]() 名学生其中数学考试情况,从中抽取了
名学生其中数学考试情况,从中抽取了![]() 名学生的数学成绩进行了统计,下面
名学生的数学成绩进行了统计,下面![]() 个判断中正确的有( )个.
个判断中正确的有( )个.
①这种调查的方式是抽样调查;②![]() 名学生是总体;③每名学生的数学成绩是个体;④
名学生是总体;③每名学生的数学成绩是个体;④![]() 名学生是总体的一个样本;⑤样本容量是
名学生是总体的一个样本;⑤样本容量是![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,完成解答过程.
(1)![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
并且用含有![]() 的式子表示发现的规律 .
的式子表示发现的规律 .
(2)根据上述方法计算:
![]()
(3)根据(1),(2)的方法,我们可以猜测下列结论:
![]() (其中
(其中![]() 均为正整数),
均为正整数),
并计算![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
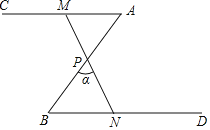
【题目】如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点共线,线段AB=20 cm,BC=8 cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.28 cm或12 cmB.28 cmC.14 cmD.14cm或6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点
,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点![]() .
.
![]() 求出点C坐标及抛物线的解析式;
求出点C坐标及抛物线的解析式;
![]() 若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
![]() 若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将
若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将![]() 沿QG翻折得到
沿QG翻折得到![]() ,当点N在坐标轴上时,求Q点的坐标.
,当点N在坐标轴上时,求Q点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com