
【题目】二次函数![]() 的图象经过点
的图象经过点![]() ,
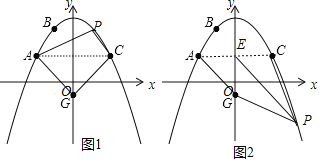
,![]() ,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点
,点A关于抛物线对称轴的对称点为点C,点P是抛物线对称轴右侧图象上的一点,点![]() .
.
![]() 求出点C坐标及抛物线的解析式;
求出点C坐标及抛物线的解析式;
![]() 若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
若以A,C,P,G为顶点的四边形面积等于30时,求点P的坐标;
![]() 若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将
若Q为线段AC上一动点,过点Q平行于y轴的直线与过点G平行于x轴的直线交于点M,将![]() 沿QG翻折得到
沿QG翻折得到![]() ,当点N在坐标轴上时,求Q点的坐标.
,当点N在坐标轴上时,求Q点的坐标.

【答案】![]() 抛物线的解析式为
抛物线的解析式为![]() ,点C的坐标为
,点C的坐标为![]() ;
;![]() P点坐标为
P点坐标为![]() 或
或![]() ;
;![]() Q点坐标为
Q点坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)用待定系数法可求得函数解析式;
(2)设![]() ,分两种情况:
,分两种情况:
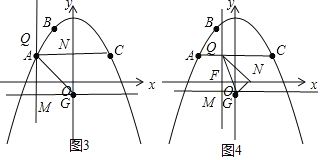
当点P在AC上方时,如图1,![]() ,解方程得P点坐标;
,解方程得P点坐标;
当点P在AC下方时,如图2,AC与y轴交于点E,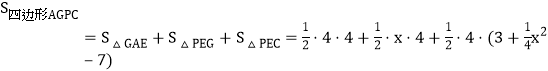 ,解方程得P点坐标;
,解方程得P点坐标;
![]() ,分3种情况:
,分3种情况:
当点N落在y轴上,如图3,
![]() 翻折得
翻折得![]() ,
,![]() ,
,![]() 点为AC与y轴的交点,
点为AC与y轴的交点,
![]() 点的坐标;
点的坐标;
当点N落在x轴上,QM与x轴交于点F,如图4,设![]()
![]() 翻折得
翻折得![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,而
,而![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,可得Q点的坐标;
,可得Q点的坐标;
当![]() ,易得Q点的坐标为
,易得Q点的坐标为![]() .
.
解:![]() 二次函数
二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,
,
![]() ,解得:
,解得: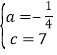 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() 二次函数
二次函数![]() 的图象的对称轴为y轴,点
的图象的对称轴为y轴,点![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() .
.
![]() 设
设![]() ,
,
当点P在AC上方时,如图1,![]() ,
,
![]() ,解得
,解得![]() ,
,![]() 舍去
舍去![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
当点P在AC下方时,如图2,AC与y轴交于点E,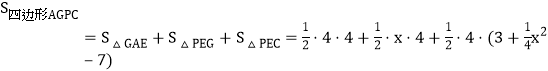 ,
,
![]() ,解得
,解得![]() ,
,![]() 舍去
舍去![]() ,此时P点坐标为
,此时P点坐标为![]() ,
,
综上所述,P点坐标为![]() 或
或![]() ;
;
![]() ,
,
当点N落在y轴上,如图3,
![]() 沿QG翻折得到
沿QG翻折得到![]() ,
,
![]() ,
,![]() ,
,
![]() 点为AC与y轴的交点,
点为AC与y轴的交点,
![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
当点N落在x轴上,QM与x轴交于点F,如图4,设![]()
![]() 沿QG翻折得到
沿QG翻折得到![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
而![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,此时Q点的坐标为
,此时Q点的坐标为![]() ,
,
当![]() ,易得Q点的坐标为
,易得Q点的坐标为![]() ,
,
综上所述,Q点坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
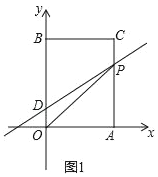
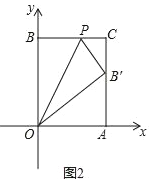
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
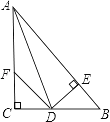
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
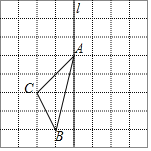
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
![]() 在图中画出与
在图中画出与![]() 关于直线l成轴对称的
关于直线l成轴对称的![]() ;
;
![]() 三角形ABC的面积为______;
三角形ABC的面积为______;
![]() 以AC为边作与
以AC为边作与![]() 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与![]() 全等;
全等;
![]() 在直线l上找一点P,使
在直线l上找一点P,使![]() 的长最短.
的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
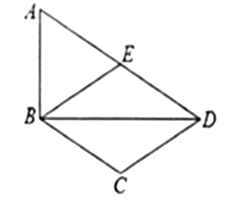
【题目】如图,在四边形ABCD中,BD为一条对角线,![]() 且
且![]() ,
,![]() ,E为AD的中点,连接BE.
,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分![]() ,
,![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
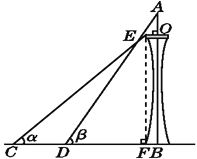
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com