
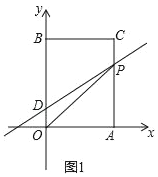
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌГЄЗНаЮOACBЕФЖЅЕуAЁЂBЗжБ№дкxжсгыyжсЩЯЃЌвбжЊOA=6ЃЌOB=10ЃЎЕуDЮЊyжсЩЯвЛЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЯпЖЮACЉCBЕФЗНЯђдЫЖЏЃЌЕБЕуPгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЕБЕуPОЙ§ЕуCЪБЃЌЧѓжБЯпDPЕФКЏЪ§НтЮіЪНЃЛ
(2)ЂйЧѓЁїOPDЕФУцЛ§SЙигкtЕФКЏЪ§НтЮіЪНЃЛ
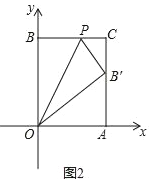
ЂкШчЭМЂкЃЌАбГЄЗНаЮбизХOPелЕўЃЌЕуBЕФЖдгІЕуBЁфЧЁКУТфдкACБпЩЯЃЌЧѓЕуPЕФзјБъЃЎ
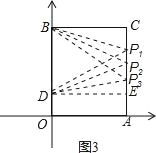
(3)ЕуPдкдЫЖЏЙ§ГЬжаЪЧЗёДцдкЪЙЁїBDPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x+2ЃЛЃЈ2ЃЉЂйSЃН6ЛђSЃНЉ2t+16ЃЛЂкЕуPЕФзјБъЪЧЃЈ
x+2ЃЛЃЈ2ЃЉЂйSЃН6ЛђSЃНЉ2t+16ЃЛЂкЕуPЕФзјБъЪЧЃЈ![]() ЃЌ10ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2
ЃЌ10ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2![]() +2ЃЉЛђЃЈ6ЃЌ10Љ2
+2ЃЉЛђЃЈ6ЃЌ10Љ2![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшжБЯпDPНтЮіЪНЮЊy=kx+bЃЌНЋDгыCзјБъДњШыЧѓГіkгыbЕФжЕЃЌМДПЩШЗЖЈГіНтЮіЪНЃЛ
ЃЈ2ЃЉЂйЕБPдкACЖЮЪБЃЌЁїODPЕзODгыИпЮЊЙЬЖЈжЕЃЌЧѓГіДЫЪБУцЛ§ЃЛЕБPдкBCЖЮЪБЃЌЕзБпODЮЊЙЬЖЈжЕЃЌБэЪОГіИпЃЌМДПЩСаГіSгыtЕФЙиЯЕЪНЃЛ
ЂкЕБDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌжБЯпOPЮЊy=xЃЌЧѓГіДЫЪБPзјБъМДПЩЃЛ
ЃЈ3ЃЉДцдкЃЌЗжБ№вдBDЃЌDPЃЌBPЮЊЕзБпШ§жжЧщПіПМТЧЃЌРћгУЙДЙЩЖЈРэМАЭМаЮгызјБъаджЪЧѓГіPзјБъМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпOAЃН6ЃЌOBЃН10ЃЌЫФБпаЮOACBЮЊГЄЗНаЮЃЌ
ЁрCЃЈ6ЃЌ10ЃЉЃЎ
ЩшДЫЪБжБЯпDPНтЮіЪНЮЊyЃНkx+bЃЌ
АбЃЈ0ЃЌ2ЃЉЃЌCЃЈ6ЃЌ10ЃЉЗжБ№ДњШыЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]()
дђДЫЪБжБЯпDPНтЮіЪНЮЊyЃН![]() x+2ЃЛ
x+2ЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкЯпЖЮACЩЯЪБЃЌODЃН2ЃЌИпЮЊ6ЃЌSЃН6ЃЛ
ЕБЕуPдкЯпЖЮBCЩЯЪБЃЌODЃН2ЃЌИпЮЊ6+10Љ2tЃН16Љ2tЃЌSЃН![]() ЁС2ЁСЃЈ16Љ2tЃЉЃНЉ2t+16ЃЛ
ЁС2ЁСЃЈ16Љ2tЃЉЃНЉ2t+16ЃЛ
ЂкЩшPЃЈmЃЌ10ЃЉЃЌдђPBЃНPBЁфЃНmЃЌШчЭМ2ЃЌ
ЁпOBЁфЃНOBЃН10ЃЌOAЃН6ЃЌ
ЁрABЁфЃН![]() ЃН8ЃЌ
ЃН8ЃЌ
ЁрBЁфCЃН10Љ8ЃН2ЃЌ
ЁпPCЃН6ЉmЃЌ
Ёрm2ЃН22+ЃЈ6ЉmЃЉ2ЃЌНтЕУmЃН![]()
дђДЫЪБЕуPЕФзјБъЪЧЃЈ![]() ЃЌ10ЃЉЃЛ
ЃЌ10ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩЮЊЃК
ШєЁїBDPЮЊЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіПМТЧЃКШчЭМ3ЃЌ
ЂйЕБBDЃНBP1ЃНOBЉODЃН10Љ2ЃН8ЃЌ
дкRtЁїBCP1жаЃЌBP1ЃН8ЃЌBCЃН6ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКCP1ЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрAP1ЃН10Љ2![]() ЃЌМДP1ЃЈ6ЃЌ10Љ2
ЃЌМДP1ЃЈ6ЃЌ10Љ2![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБBP2ЃНDP2ЪБЃЌДЫЪБP2ЃЈ6ЃЌ6ЃЉЃЛ
ЂлЕБDBЃНDP3ЃН8ЪБЃЌ
дкRtЁїDEP3жаЃЌDEЃН6ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКP3EЃН![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрAP3ЃНAE+EP3ЃН2![]() +2ЃЌМДP3ЃЈ6ЃЌ2
+2ЃЌМДP3ЃЈ6ЃЌ2![]() +2ЃЉЃЌ
+2ЃЉЃЌ
злЩЯЃЌТњзуЬтвтЕФPзјБъЮЊЃЈ6ЃЌ6ЃЉЛђЃЈ6ЃЌ2![]() +2ЃЉЛђЃЈ6ЃЌ10Љ2
+2ЃЉЛђЃЈ6ЃЌ10Љ2![]() ЃЉЃЎ
ЃЉЃЎ
ЕуОІЁПДЫЬтЪєгквЛДЮКЏЪ§злКЯЬтЃЌЩцМАЕФжЊЪЖгаЃКД§ЖЈЯЕЪ§ЗЈШЗЖЈвЛДЮКЏЪ§НтЮіЪНЃЌзјБъгыЭМаЮаджЪЃЌЕШбќШ§НЧаЮЕФЖЈвхЃЌЙДЙЩЖЈРэЃЌРћгУСЫЗжРрЬжТлЕФЫМЯыЃЌЪьСЗеЦЮеД§ЖЈЯЕЪ§ЗЈЪЧНтБОЬтЕквЛЮЪЕФЙиМќЃЎ


 жаПМРћНЃжаПМЪдОэЛуБрЯЕСаД№АИ
жаПМРћНЃжаПМЪдОэЛуБрЯЕСаД№АИ НЬг§ЪРМвзДдЊОэЯЕСаД№АИ
НЬг§ЪРМвзДдЊОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌPЪЧЖдНЧЯпBDЩЯЕФвЛЕуЃЌЙ§ЕуCзїCQЁЮDBЃЌЧвCQ=DPЃЌСЌНгAPЁЂBQЁЂPQЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAPDЁеЁїBQCЃЛ
ЃЈ2ЃЉШєЁЯABP+ЁЯBQC=180ЁуЃЌЧѓжЄЃКЫФБпаЮABQPЮЊСтаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
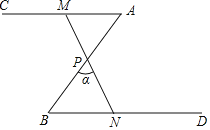
ЁОЬтФПЁПШчЭМЃЌЁЯA=ЁЯB=50ЁуЃЌPЮЊABжаЕуЃЌЕуMЮЊЩфЯпACЩЯЃЈВЛгыЕуAжиКЯЃЉЕФШЮвтЕуЃЌСЌНгMPЃЌВЂЪЙMPЕФбгГЄЯпНЛЩфЯпBDгкЕуNЃЌЩшЁЯBPN=ІСЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAPMЁеЁїBPNЃЛ
ЃЈ2ЃЉЕБMN=2BNЪБЃЌЧѓІСЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєЁїBPNЕФЭтаФдкИУШ§НЧаЮЕФФкВПЃЌжБНгаДГіІСЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊAЃЌBЃЌCШ§ЕуЙВЯпЃЌЯпЖЮABЃН20 cmЃЌBCЃН8 cmЃЌЕуEЃЌFЗжБ№ЪЧЯпЖЮABЃЌBCЕФжаЕуЃЌдђЯпЖЮEFЕФГЄЮЊЃЈ ЃЉ
A.28 cmЛђ12 cmB.28 cmC.14 cmD.14cmЛђ6 cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбЦНУцФквЛЬѕЪ§жсxШЦдЕуOФцЪБеыа§зЊНЧІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЕУЕНСэвЛЬѕЪ§жсyЃЌxжсКЭyжсЙЙГЩвЛИіЦНУцаБзјБъЯЕЃЎЙцЖЈЃКЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛxжсгкЕуAЃЌЙ§ЕуPзїxжсЕФЦНааЯпЃЌНЛyжсгкЕуBЃЌШєЕуAдкxжсЩЯЖдгІЕФЪЕЪ§ЮЊaЃЌЕуBдкyжсЩЯЖдгІЕФЪЕЪ§ЮЊbЃЌдђГЦгаађЪЕЪ§ЖдЃЈaЃЌbЃЉЮЊЕуPЕФаБзјБъЃЌдкФГЦНУцаБзјБъЯЕжаЃЌвбжЊІШ=60ЁуЃЌЕуMЁфЕФаБзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌЕуNгыЕуMЙигкyжсЖдГЦЃЌдђЕуNЕФаБзјБъЮЊ_____ЃЎ
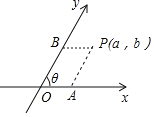
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
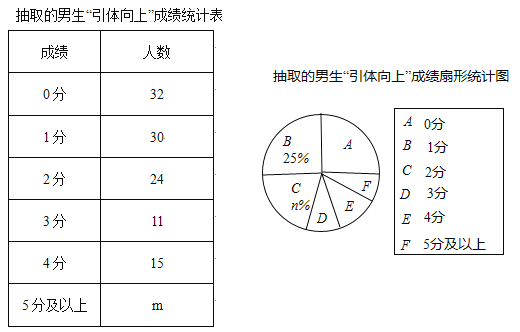
ЁОЬтФПЁПФГЪаУїФъЕФГѕжаБЯвЕЩ§бЇПМЪдЃЌФтНЋЁАв§ЬхЯђЩЯЁБзїЮЊФаЩњЬхг§ПМЪдЕФвЛИіБиПМЯюФПЃЌТњЗжЮЊ10ЗжЃЎгаЙиВПУХЮЊЬсЧАСЫНтУїФъВЮМгГѕжаБЯвЕЩ§бЇПМЪдЕФФаЩњЕФЁАв§ЬхЯђЩЯЁБЫЎЦНЃЌдкШЋЪаАЫФъМЖФаЩњжаЫцЛњГщШЁСЫВПЗжФаЩњЃЌЖдЫћУЧЕФЁАв§ЬхЯђЩЯЁБЫЎЦННјааВтЪдЃЌВЂНЋВтЪдНсЙћЛцжЦГЩШчЯТЭГМЦЭМБэЃЈВПЗжаХЯЂЮДИјГіЃЉЃК
ЧыФуИљОнЭГМЦЭМБэжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЃКm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаDзщЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉФПЧАИУЪаАЫФъМЖгаФаЩњ3600УћЃЌЧыЙРМЦЦфжаЁАв§ЬхЯђЩЯЁБЕУСуЗжЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
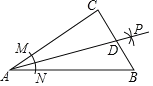
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌвдЖЅЕуAЮЊдВаФЃЌЪЪЕБГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛACЁЂABгкЕуMЁЂNЃЌдйЗжБ№вдЕуMЁЂNЮЊдВаФЃЌДѓгк![]() MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌзїЩфЯпAPНЛБпBCгкЕуD,ШєACЃН24ЃЌABЃН30ЃЌЧв
MNЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌзїЩфЯпAPНЛБпBCгкЕуD,ШєACЃН24ЃЌABЃН30ЃЌЧв![]() ЃН216ЃЌдђЁїABDЕФУцЛ§ЪЧ( )
ЃН216ЃЌдђЁїABDЕФУцЛ§ЪЧ( )
A.105B.120
C.135D.115
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌЕуAЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕуCЃЌЕуPЪЧХзЮяЯпЖдГЦжсгвВрЭМЯѓЩЯЕФвЛЕуЃЌЕу
ЃЌЕуAЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЮЊЕуCЃЌЕуPЪЧХзЮяЯпЖдГЦжсгвВрЭМЯѓЩЯЕФвЛЕуЃЌЕу![]() ЃЎ
ЃЎ
![]() ЧѓГіЕуCзјБъМАХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓГіЕуCзјБъМАХзЮяЯпЕФНтЮіЪНЃЛ
![]() ШєвдAЃЌCЃЌPЃЌGЮЊЖЅЕуЕФЫФБпаЮУцЛ§ЕШгк30ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ШєвдAЃЌCЃЌPЃЌGЮЊЖЅЕуЕФЫФБпаЮУцЛ§ЕШгк30ЪБЃЌЧѓЕуPЕФзјБъЃЛ
![]() ШєQЮЊЯпЖЮACЩЯвЛЖЏЕуЃЌЙ§ЕуQЦНаагкyжсЕФжБЯпгыЙ§ЕуGЦНаагкxжсЕФжБЯпНЛгкЕуMЃЌНЋ
ШєQЮЊЯпЖЮACЩЯвЛЖЏЕуЃЌЙ§ЕуQЦНаагкyжсЕФжБЯпгыЙ§ЕуGЦНаагкxжсЕФжБЯпНЛгкЕуMЃЌНЋ![]() биQGЗелЕУЕН
биQGЗелЕУЕН![]() ЃЌЕБЕуNдкзјБъжсЩЯЪБЃЌЧѓQЕуЕФзјБъЃЎ
ЃЌЕБЕуNдкзјБъжсЩЯЪБЃЌЧѓQЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќRtЁїABCжаЃЌЁЯBACЃН90ЁуЃЌADЁЭBCгкЕуDЃЌЁЯABCЕФЦНЗжЯпЗжБ№НЛACЁЂADгкEЁЂFСНЕуЃЌMЮЊEFЕФжаЕуЃЌAMЕФбгГЄЯпНЛBCгкЕуNЃЌСЌНгDMЃЌЯТСаНсТлЃКЂйAEЃНAFЃЛЂкDFЃНDNЃЛЂлANЃНBFЃЛЂмENЁЭNCЃЛЂнAEЃНNCЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
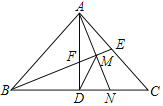
A. 2ИіB. 3ИіC. 4ИіD. 5Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com