
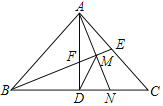
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①AE=AF;②DF=DN;③AN=BF;④EN⊥NC;⑤AE=NC,其中正确结论的个数是( )
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
①根据等腰直角三角形的性质及角平分线的定义求得![]() ,继而可得∠AFE=∠AEB=67.5°,即可判断①;
,继而可得∠AFE=∠AEB=67.5°,即可判断①;
②求出BD=AD,∠DBF=∠DAN,∠BDF=∠ADN,证△DFB≌△DAN,即可判断②;
③根据A、B、D、M四点共圆求出∠ADM=22.5°,根据三角形外角性质求出∠DNM,求出∠MDN=∠DNM,即可判断③;
④求出∠BMD=45°=∠BMN,即可判断④;
⑤证明△AFB≌△CNA可得AF=CN,由AF=AE,即可判断⑤.
解:∵等腰Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD=∠CAD=∠C=45°,
∵∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠AEF=∠CBE+∠C=22.5°+45°=67.5°,∠AFE=∠FBA+∠BAF=22.5°+45°=67.5°
∴∠AEF=∠AFE,
∴AE=AF,
故①正确;
∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°,
∴AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,AM⊥BE,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中
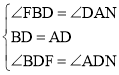 ,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,AN=BF,
∴②③正确;
连接EN,
∵AE=AF,FM=EM,
∴AM⊥EF,
∴∠BMA=∠BMN=90°,
∵BM=BM,∠MBA=∠MBN,
∴△MBA≌△MBN,
∴AM=MN,
∴BE垂直平分线段AN,
∴AB=BN,EA=EN,
∵BE=BE,
∴△ABE≌△NBE,
∴∠ENB=∠EAB=90°,
∴EN⊥NC.
故④正确;
在△AFB和△CNA中,
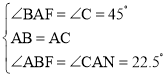 ,
,
∴△AFB≌△CAN(ASA),
∴AF=CN,
∵AF=AE,
∴AE=CN,
故⑤正确;
其中正确结论的个数是:①②③④⑤,共5个;
故选:D.


科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
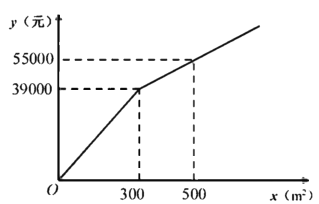
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.

请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=![]() ∠AEF,∠___=
∠AEF,∠___= ![]() ∠EFD(____________)
∠EFD(____________)
∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种学生用计算器,进价为每台20元,售价为每台30元时,每周可卖160台,如果每台售价每上涨2元,每周就会少卖20台,但厂家规定最高每台售价不能超过33元,当计算器定价为多少元时,商场每周的利润恰好为1680元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,百位数是![]() ,十位数是
,十位数是![]() ,个位数是
,个位数是![]() ,我们可以记作
,我们可以记作![]() ,
, ![]() 表示,例如
表示,例如![]() ,仿照上面的例子,
,仿照上面的例子,
(1)![]() 可以用 表示;
可以用 表示;
(2)![]() 可以用 表示;
可以用 表示;
(3)欧阳老师给4为同学玩一个数字游戏,先请A同学心里想一个三位数,并把这个三位数在纸上写两遍构成一个六位数交给B同学,如他心里想的是789,那么他在纸上写的就是789789,B把这个六位数除以7,得到的商写在另一张纸上并交给C同学,C同学把B同学给他的数字除以11,得到的商写在另一张纸上并交给D同学,D同学把C同学给他的数字除以13,得到的商写在另一张纸上,并交还给A同学,还给![]() 同学的数字和他刚开始想的数字有什么关系?并说明理由.
同学的数字和他刚开始想的数字有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com